

 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;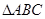 中,A、B、C分别为三边
中,A、B、C分别为三边 所对的角,若
所对的角,若 ,求
,求 的最大值.
的最大值.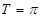 ,函数的单调递增区间为
,函数的单调递增区间为 ;(2)因此
;(2)因此 的最大值为
的最大值为 .
. 的解析式第一、三项结合,利用二倍角的余弦函数公式化简,第二项利用二倍角的正弦函数公式化简,合并后提取
的解析式第一、三项结合,利用二倍角的余弦函数公式化简,第二项利用二倍角的正弦函数公式化简,合并后提取 ,再利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,找出
,再利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,找出 的值,代入周期公式
的值,代入周期公式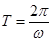 ,即可求出函数的最小正周期,由正弦函数的递增区间列出关于
,即可求出函数的最小正周期,由正弦函数的递增区间列出关于 的不等式,求出不等式的解集即可得到
的不等式,求出不等式的解集即可得到 的递增区间;(2)由
的递增区间;(2)由 及确定出的
及确定出的 的解析式,变形后利用特殊角的三角函数值求出
的解析式,变形后利用特殊角的三角函数值求出 的度数,可得出
的度数,可得出 的值,再由
的值,再由 的值,利用余弦定理列出关系式,将
的值,利用余弦定理列出关系式,将 与
与 的值代入,利用完全平方公式变形后,再利用基本不等式即可求出
的值代入,利用完全平方公式变形后,再利用基本不等式即可求出 的最大值.
的最大值.
 , 3分
, 3分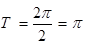 . 4分
. 4分 得
得
 . 6分
. 6分 可得
可得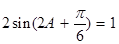 ,又
,又 ,所以
,所以 。8分
。8分 ,即
,即 又
又 ,所以
,所以 ,故
,故 ,当且仅当
,当且仅当 ,即
,即 时等号成立
时等号成立 的最大值为
的最大值为 . 12分
. 12分

科目:高中数学 来源:不详 题型:解答题
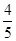 ,求S△AOB.
,求S△AOB.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
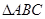 中,
中,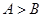 是
是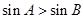 成立的充要条件;
成立的充要条件; 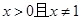 时,有
时,有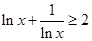 ;
;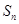 是等差数列
是等差数列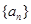 的前n项和,若
的前n项和,若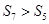 ,则
,则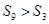 ;
;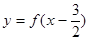 为R上的奇函数,则函数
为R上的奇函数,则函数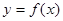 的图象一定关于点
的图象一定关于点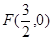 成中心对称.
成中心对称.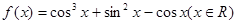 有最大值为
有最大值为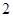 ,有最小值为0。
,有最小值为0。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
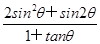 =k,0<θ<
=k,0<θ<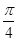 ,则sinθ-
,则sinθ-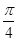 的值( )
的值( )| A.随着k的增大而增大 |
| B.有时随着k的增大而增大,有时随着k的增大而减小 |
| C.随着k的增大而减小 |
| D.是一个与k无关的常数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com