
(1) ![]() +
+![]() =3
=3![]() -
-![]() ;?
;?
(2) ![]() =4
=4![]() -
-![]() -
-![]() .?
.?
解法一:(1)原式可变形为
![]() =
=![]() +(
+(![]() -
-![]() )+(
)+(![]() -
-![]() )=
)= ![]() +
+![]() +
+![]() .?
.?
由共面向量定理的推论知P与A、B、M?共面?.?
(2)原式可变形为![]() =2
=2![]() +
+![]() -
-![]() +
+![]() -
-![]()
=2![]() +
+![]() +
+![]() .
.
由共面向量定理的推论可得
P位于平面ABM内的充要条件可写成![]() =
=![]() +x
+x![]() +y
+y![]() .
.
而此题推得![]() =2
=2![]() +
+![]() +
+![]() ,?
,?
∴P与A、B、M不共面.?
解法二:(1)原式可变形为
![]() =3
=3![]() -
-![]() -
-![]() .?
.?
∵3+(-1)+(-1)=1,?
∴B与P、A、M共面,?
即P与A、B、M共面.?
(2)![]() =4
=4![]() -
-![]() -
-![]() ,
,
∵4+(-1)+(-1)=2≠1,?
∴P与A、B、M不共面.?
温馨提示:判断点P是否位于平面MAB内,关键是看向量![]() 能否用向量
能否用向量![]() 、
、![]() 表示(或看向量
表示(或看向量![]() 是否能写成
是否能写成![]() +x
+x![]() +y
+y![]() 的形式).当
的形式).当![]() 能用
能用![]() 、
、![]() 表示时,P位于平面MAB内;当
表示时,P位于平面MAB内;当![]() 不能用
不能用![]() 、
、![]() 表示时,P不在平面MAB内.当
表示时,P不在平面MAB内.当![]() =x
=x![]() +?y
+?y![]() +z
+z![]() 时,P与M、A、B共面的充要条件是x+ y+ z=1.本例利用这个结论判断P与M、A、B是否共面更简便.
时,P与M、A、B共面的充要条件是x+ y+ z=1.本例利用这个结论判断P与M、A、B是否共面更简便.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源:设计选修数学2-1苏教版 苏教版 题型:044
已知A、B、M三点不共线,对于平面ABM外的任一点O,确定下列各条件下,点P是否与A、B、M一定共面.
(1)![]() +
+![]() =3
=3![]() -
-![]() ;
;
(2)![]() =4
=4![]() -
-![]() -
-![]() .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012年湖南省衡阳市高二第三次月考考试理科数学 题型:选择题
已知A、B、M三点不共线,对于平面ABM外任一点O,若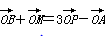 ,则点P与A、B、M( )
,则点P与A、B、M( )
A.共面 B.共线
C.不共面 D.不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com