
已知四边形 满足
满足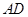 ∥
∥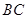 ,
, ,
,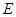 是
是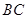 的中点,将
的中点,将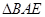 沿着
沿着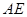 翻折成
翻折成 ,使面
,使面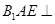 面
面 ,
,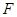 为
为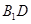 的中点.
的中点.

(Ⅰ)求四棱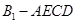 的体积;(Ⅱ)证明:
的体积;(Ⅱ)证明: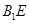 ∥面
∥面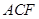 ;
;
(Ⅲ)求面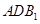 与面
与面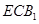 所成二面角的余弦值.
所成二面角的余弦值.
科目:高中数学 来源: 题型:
| AB |
| BC |
| CB |
| CD |
| CD |
| DA |
| DA |
| AB |
| A、平行四边形 | B、梯形 |
| C、平面四边形 | D、空间四边形 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 在平面直角坐标系xoy中,已知四边形OABC是平行四边形,A(4,0),C(1,
在平面直角坐标系xoy中,已知四边形OABC是平行四边形,A(4,0),C(1,| 3 |
| OA |
| OP |
| CM |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高三上学期期中考试理科数学试卷(解析版) 题型:解答题
(本题满分14分)已知四边形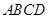 满足
满足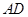 ∥
∥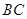 ,
,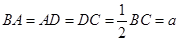 ,
,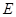 是
是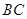 的中点,将
的中点,将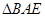 沿着
沿着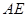 翻折成
翻折成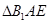 ,使面
,使面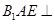 面
面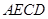 ,
,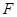 为
为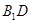 的中点.
的中点.
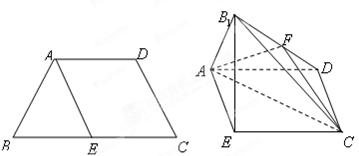
(Ⅰ)求四棱锥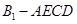 的体积;(Ⅱ)证明:
的体积;(Ⅱ)证明: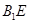 ∥面
∥面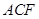 ;
;
(Ⅲ)求面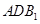 与面
与面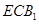 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省豫北六校高三第二次精英联赛考试理科数学试卷 题型:解答题
已知四边形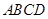 满足
满足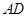 ∥
∥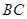 ,
,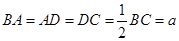 ,
,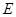 是
是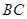 的中点,将
的中点,将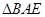 沿着
沿着 翻折成
翻折成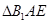 ,使面
,使面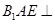 面
面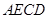 ,
,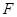 为
为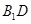 的中点.
的中点.
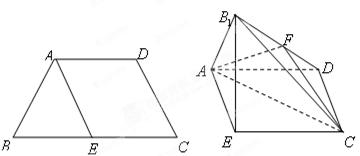
(Ⅰ)求四棱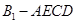 的体积;
的体积;
(Ⅱ)证明: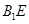 ∥面
∥面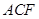 ;
;
(Ⅲ)求面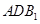 与面
与面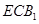 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com