
已知正方形![]()
![]()
![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,如图所示,记二面角
折起,如图所示,记二面角![]() 的大小为
的大小为![]()
![]()
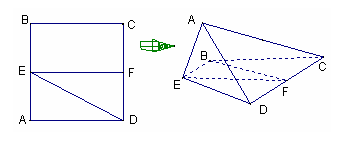 (I) 证明
(I) 证明![]() 平面
平面![]() ;
;
(II)若![]() 为正三角形,试判断点
为正三角形,试判断点![]() 在平面
在平面![]() 内的射影
内的射影![]() 是否在直线
是否在直线![]() 上,证明你的结论,并求角
上,证明你的结论,并求角![]() 的余弦值
的余弦值![]()
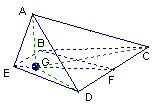 分析:充分发挥空间想像能力,重点抓住不变的位置和数量关系,借助模型图形得出结论,并给出证明.
分析:充分发挥空间想像能力,重点抓住不变的位置和数量关系,借助模型图形得出结论,并给出证明.
解: (I)证明:EF分别为正方形ABCD得边AB、CD的中点,
![]() EB//FD,且EB=FD,
EB//FD,且EB=FD,
![]() 四边形EBFD为平行四边形
四边形EBFD为平行四边形![]()
![]() BF//ED.
BF//ED.
![]() ,
,![]()
![]() 平面
平面![]()
![]()
(II)如右图,点A在平面BCDE内的射影G在直线EF上,过点A作AG垂直于平面BCDE,垂足为G,连结GC,GD![]()
![]()
![]() ACD为正三角形,
ACD为正三角形,![]() AC=AD.
AC=AD.
![]() CG=GD.
CG=GD.
![]() G在CD的垂直平分线上,
G在CD的垂直平分线上, ![]() 点A在平面BCDE内的射影G在直线EF上,
点A在平面BCDE内的射影G在直线EF上,
过G作GH垂直于ED于H,连结AH,则![]() ,所以
,所以![]() 为二面角A-DE-C的平面角
为二面角A-DE-C的平面角![]() 即
即![]() .
.
设原正方体的边长为2a,连结AF,在折后图的![]() AEF中,AF=
AEF中,AF=![]() ,EF=2AE=2a,即
,EF=2AE=2a,即![]() AEF为直角三角形,
AEF为直角三角形, ![]() .
.
![]() 在Rt
在Rt![]() ADE中,
ADE中, ![]()
![]() .
.
![]() ,
,![]()
![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
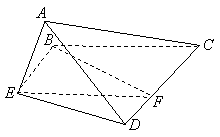
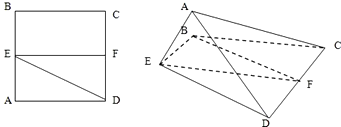 已知正方形ABCD.E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为θ(0<θ<π).
已知正方形ABCD.E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为θ(0<θ<π).查看答案和解析>>
科目:高中数学 来源: 题型:
(06年辽宁卷)(12分)
已知正方形![]() ,
,![]() 分别是边
分别是边![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,如图所示,记二面角
折起,如图所示,记二面角![]() 的大小为
的大小为![]() (
(![]() ).
).
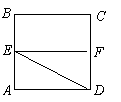
(1)证明![]() 平面
平面![]() ;
;
(2)若![]() 为正三角形,试判断点
为正三角形,试判断点![]() 在平面
在平面![]() 内的射影
内的射影![]() 是否在直线
是否在直线![]() 上,证明你的结论,并求角
上,证明你的结论,并求角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(I) 证明![]() 平面
平面![]() ;
;
(II)若![]() 为正三角形,试判断点
为正三角形,试判断点![]() 在平面
在平面![]() 内的射影
内的射影![]() 是否在直线
是否在直线![]() 上,证明你的结论,并求角
上,证明你的结论,并求角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
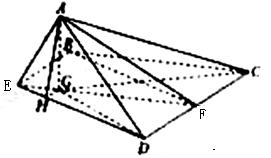
(1)证明![]() 平面
平面![]() ;
;
(2)若![]() 为正三角形,试判断点
为正三角形,试判断点![]() 在平面
在平面![]() 内的射影
内的射影![]() 是否在直线
是否在直线![]() 上,证明你的结论,并求角
上,证明你的结论,并求角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com