
| A. | 36 | B. | 32 | C. | 16 | D. | 8 |
分析 先根据基本不等式的性质得到ab≥1,再由题意得到2a+b=3ab,即可求出(a+1)(b+9)的最小值.
解答 解:正实数a,b满足$\frac{1}{a}+\frac{9}{b}=6$,
∴6=$\frac{1}{a}$+$\frac{9}{b}$≥2$\sqrt{\frac{9}{ab}}$,
即$\sqrt{ab}$≥1,当且仅当$\frac{1}{a}$=$\frac{9}{b}$时,即a=$\frac{1}{3}$,b=3时取等号,
∵$\frac{1}{a}+\frac{9}{b}=6$,
∴b+9a=6ab,
∴(a+1)(b+9)=9a+b+ab+9=7ab+9≥7+9=16,
故(a+1)(b+9)的最小值是16,
故选:C.
点评 本题主要考查基本不等式在最值中的应用,要注意检验等号成立条件是否具备,属于基础题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:选择题
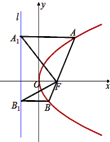 如图,过抛物线C:y2=2px(p>0)的焦点F作直线交C于A、B两点,过A、B分别向C的准线l作垂线,垂足为A1、B1,已知△AA1F与△BB1F的面积分别为9和1,则△A1B1F的面积为( )
如图,过抛物线C:y2=2px(p>0)的焦点F作直线交C于A、B两点,过A、B分别向C的准线l作垂线,垂足为A1、B1,已知△AA1F与△BB1F的面积分别为9和1,则△A1B1F的面积为( )| A. | 4 | B. | 6 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | [-2,+∞) | C. | (-2,+∞) | D. | [-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 形式正确,结论正确 | B. | 形式错误,结论错误 | ||
| C. | 形式正确,结论错误 | D. | 形式错误,结论正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $-\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com