
分析 (1)由等差数列2,6,10,…190的公差为4,等差数列2,8,14,…,200的公差为6,得到由这两个等差数列的公共项组成一个新数列公差为12,由此能求出这个新数列{an}的通项公式.
(2)根据条件求出这个新数列{an}的项数,再利用求和公式求得它的各项和.
解答 解:(1)设两个等差数列2,6,10,…,190,及2,8,14,…,200的通项公式分别为bn和 cn,
则易知:bn=4n-2( 1≤n≤48,n∈N*),cn=6n-4 (1≤n≤34,n∈N* ).
设 bn=cm,即 4n-2=6m-4,则 n=m+$\frac{m-1}{2}$∈N*,
故m=2k-1,k∈N+,k≤16,{an}是以c1为首相,以12为公差的等差数列.
∴an=2+12(n-1)=12n-10.
(2)设新数列{an}的前n项和为Sn,∵新数列最大项满足 an≤190,
∴2+(n-1)×12≤190,解得n≤$\frac{50}{3}$,∴n=16.
∵新数列中第16项a16=2+(16-1)×12=182,
新数列{an}的各项为:2,14,26,…,182,
∴{an}的各项之和为S16=$\frac{16(2+182)}{2}$=1472.
点评 本题考查等差数列的前n项和的求法,解题时要认真审题,注意等差数列的基本性质的合理运用,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,且过点$({2,\sqrt{2}})$,四边形ABCD的顶点在椭圆E上,且对角线AC,BD过原点O,${k_{AC}}•{k_{BD}}=-\frac{b^2}{a^2}$.
如图,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,且过点$({2,\sqrt{2}})$,四边形ABCD的顶点在椭圆E上,且对角线AC,BD过原点O,${k_{AC}}•{k_{BD}}=-\frac{b^2}{a^2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36 | B. | 32 | C. | 16 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 240 | B. | 360 | C. | 480 | D. | 720 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
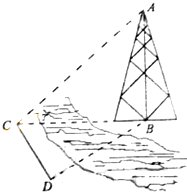 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.现测得∠BCD=75°,∠BDC=60°,CD=20,并在点C测得塔顶A的仰角为45°,则塔高AB为$10\sqrt{6}$.
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.现测得∠BCD=75°,∠BDC=60°,CD=20,并在点C测得塔顶A的仰角为45°,则塔高AB为$10\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com