
分析 (1)利用导数得出函数f(x)的极值点x0,再令g′(x0)=0即可得出a的值,再进行验证即可;
(2)通过对k-1分正负讨论,把要证明的不等式变形等价转化,再利用导数研究其极值与最值即可.
解答 解:(1)∵f(x)=-x2+2blnx,g(x)=x+$\frac{1}{x}$,
∴x>0,
g′(x)=1-$\frac{1}{{x}^{2}}$,令g′(x)=0,解得:x=1,
故x=1是f(x)的极值点,
而f′(x)=-2x+$\frac{2b}{x}$,故f′(1)=-2+2b=0,解得:b=1;
经检验,b=1,符合题意.
(2)令h(x)=f(x)-g(x)=-x2+2lnx-x-$\frac{1}{x}$,x∈[$\frac{1}{e}$,3].
则h′(x)=-2x+$\frac{2}{x}$-1+$\frac{1}{{x}^{2}}$=-$\frac{(x+1)(2x+1)(x-1)}{{x}^{2}}$,令h′(x)=0,解得x=1.
当x∈[$\frac{1}{e}$,1)时,h′(x)>0,函数h(x)单调递增;当x∈(1,3]时,h′(x)<0,函数h(x)单调递减.
∴当x=1时,函数h(x)取得极大值h(1)=-3.h(3)=-$\frac{37}{3}$+2ln3,h($\frac{1}{e}$)=-e-2-$\frac{1+e}{{e}^{2}}$,可知:h(3)<h($\frac{1}{e}$).
①当k-1>0时,对于?x1,x2∈[$\frac{1}{e}$,3],不等式 $\frac{{f({x_1})-g({x_2})}}{k-1}$≤1恒成立,
等价于k-1≥[f(x1)-g(x2)]max,∵f(x1)-g(x2)≤f(1)-g(1)=-3,
∴k≥-3+1=-2,又k>1,∴k>1.
②当k-1<0时,对于?x1,x2∈[$\frac{1}{e}$,3],不等式 $\frac{{f({x_1})-g({x_2})}}{k-1}$≤1恒成立,
等价于k-1≤[f(x1)-g(x2)]min,
∵f(x1)-g(x2)≥f(3)-g(3)=-$\frac{37}{3}$+2ln3,
∴k≤-$\frac{34}{3}$+2ln3,
又∵k≤1,∴k≤-$\frac{34}{3}$+2ln3.
综上可知:实数k的取值范围是(-∞,-$\frac{34}{3}$+ln3]∪(1,+∞).
点评 本题考查了利用导数研究函数的单调性、极值、证明不等式,考查了分类讨论的思想方法,考查了计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
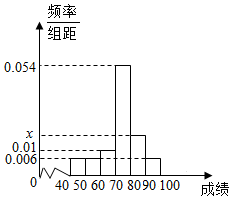 如图是某班50位学生期中考试化学成绩的频率分布直方图,其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],则成绩在[70,90)内的频数为( )
如图是某班50位学生期中考试化学成绩的频率分布直方图,其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],则成绩在[70,90)内的频数为( )| A. | 27 | B. | 30 | C. | 32 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ρ=1 | B. | ρsinθ=1 | C. | ρcosθ=1 | D. | ρ=2sinθ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
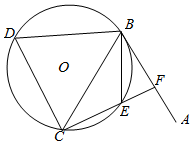 如图所示,直线AB为圆O的切线,切点为B,点C在圆O上,∠ABC的平分线BE交圆O于点E,DB垂直BE交圆O于点D.
如图所示,直线AB为圆O的切线,切点为B,点C在圆O上,∠ABC的平分线BE交圆O于点E,DB垂直BE交圆O于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
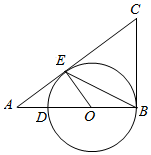 如图,E为⊙O上一点,点A在直径BD的延长线上,过点B作⊙O的切线交AE的延长线于点C,CE=CB.
如图,E为⊙O上一点,点A在直径BD的延长线上,过点B作⊙O的切线交AE的延长线于点C,CE=CB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | -2 | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 做不到光盘 | 能做到光盘 | 合计 | |
| 男 | 45 | 10 | 55 |
| 女 | 30 | 15 | 45 |
| 合计 | 75 | 25 | 100 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| K0 | 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com