
分析 根据指数函数的图象与性质,化简不等式,求出它的解集即可.
解答 解:原不等式可化为${(\frac{1}{2})}^{{x}^{2}+x}$>${(\frac{1}{2})}^{{2x}^{2}-mx+m+4}$,…(2分)
因为函数y=${(\frac{1}{2})}^{x}$在R上是减函数,
所以x2+x>2x2-mx+m+4在R上恒成立,
即x2-(m+1)x+m+4>0对x∈R恒成立,…(6分)
所以△=[-(m+1)]2-4(m+4)<0,
即m2-2m-15<0,解得-3<m<5,
所以实数m的取值范围是(-3,5).…(10分)
点评 本题考查了利用指数函数的单调性求不等式的应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=(x+1)2,x∈(0,+∞) | B. | y=log${\;}_{\frac{1}{2}}$x,x∈(1,+∞) | ||
| C. | y=2x-1 | D. | y=$\sqrt{2x-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
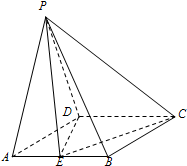 在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PA=PD=2,PD⊥CD.E为AB中点.
在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PA=PD=2,PD⊥CD.E为AB中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3] | B. | (-∞,-3) | C. | [43,+∞) | D. | (-3,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校高二奥赛班N名学生的物理测评成绩(满分120分)分布直方图如图,已知分数在100-110的学生数有21人.
某校高二奥赛班N名学生的物理测评成绩(满分120分)分布直方图如图,已知分数在100-110的学生数有21人.| 数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
| 物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com