解:(1)
(2)当a=100时,由题意知数列{a
n}的前34项成首项为100,公差为-3的等差数列,从第35项开始,奇数项均为3,偶数项均为1,
从而S
100=(100+97+94+…+4+1)+(3+1+…+3+1)(前一组共34项,后一组共66项)
=
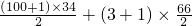
=1717+132
=1849.
(3)当

时,因为
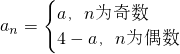
,
所以
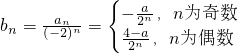
,
当n=2k,k∈N
*时,
T
n=b
1+b
2+…+b
2k=
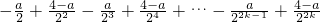
=-
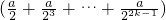

=-
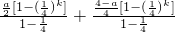
=
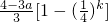
.
因为1<a<

,所以

,
当n=2k-1,k∈N
*时,
T
n=b
1+b
2+…+b
2k-1=
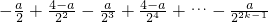
<

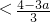
.
所以
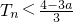
.
分析:解:(1)当a=100时,由题意知数列{a
n}的前34项成首项为100,公差为-3的等差数列,从第35项开始,奇数项均为3,偶数项均为1,由此能完成表格.
(2)当a=100时,由题意知数列{a
n}的前34项成首项为100,公差为-3的等差数列,从第35项开始,奇数项均为3,偶数项均为1,从而S
100=(100+97+94+…+4+1)+(3+1+…+3+1)(前一组共34项,后一组共66项),由此能求出结果.
(3)当

时,因为
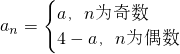
,所以
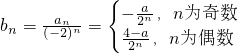
,由此能够证明当

时,
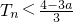
.
点评:本题考查数列与函数的综合运用.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.本题的易错点是不区分n的奇偶性,导致出错.

 ,
,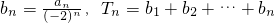 ,求证:当
,求证:当 时,
时,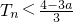 .
. 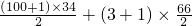
 时,因为
时,因为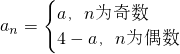 ,
,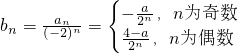 ,
,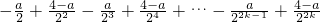
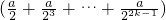

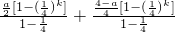
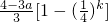 .
. ,所以
,所以 ,
,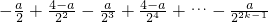

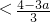 .
.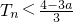 .
. 时,因为
时,因为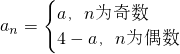 ,所以
,所以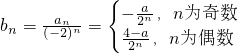 ,由此能够证明当
,由此能够证明当 时,
时,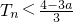 .
.

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案