
【题目】下列各式:
(1)![]() ;
;
(2)已知![]() ,则
,则![]() ;
;
(3)函数![]() 的图象与函数
的图象与函数![]() 的图象关于y轴对称;
的图象关于y轴对称;
(4)函数![]() 的定义域是R,则m的取值范围是
的定义域是R,则m的取值范围是![]() ;
;
(5)函数![]() 的递增区间为
的递增区间为![]() .
.
正确的有______________________.(把你认为正确的序号全部写上)
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]()
(1)化![]() 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若![]() 上的点P对应的参数为
上的点P对应的参数为![]() ,Q为
,Q为![]() 上的动点,求PQ的中点M到直线
上的动点,求PQ的中点M到直线![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() 且满足
且满足![]() ,数列
,数列![]() 中,
中,![]() 对任意正整数
对任意正整数![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在实数![]() ,使得数列
,使得数列![]() 是等比数列?若存在,请求出实数
是等比数列?若存在,请求出实数![]() 及公比
及公比![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() 相切.
相切.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 截圆
截圆![]() 所得弦长为
所得弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)设圆![]() 与
与![]() 轴的负半抽的交点为
轴的负半抽的交点为![]() ,过点
,过点![]() 作两条斜率分别为
作两条斜率分别为![]() 的直线交圆
的直线交圆![]() 于
于![]() 两点,且
两点,且![]() ,证明:直线
,证明:直线![]() 过定点,并求出该定点坐标.
过定点,并求出该定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题P;实数x满足x2-4ax+3a2<0,其中a>0;命题q:实数x满足x2-5x+6≤0
(1)若a=1,且![]() 为真命题,求实数x的取值范围。
为真命题,求实数x的取值范围。
(2)若p是q成立的必要不充分条件,求实数a 的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通常表明地震能量大小的尺度是里氏震级,其计算公式为:![]() ,其中,
,其中,![]() 是被测地震的最大振幅,
是被测地震的最大振幅,![]() 是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差)。
是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差)。
(1)假设在一次地震中,一个距离震中100千米的测震仪记录的地震最大振幅是30,此时标准地震的振幅是0.001,计算这次地震的震级(精确到0.1);
(2)5级地震给人的震感已比较明显,计算8级地震的最大振幅是5级地震的最大振幅的多少倍?
(以下数据供参考:![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,某城市有一块半径为40![]() 的半圆形(以
的半圆形(以![]() 为圆心,
为圆心,![]() 为直径)绿化区域,现计划对其进行改建,在
为直径)绿化区域,现计划对其进行改建,在![]() 的延长线上取点
的延长线上取点![]() ,使
,使![]() ,在半圆上选定一点
,在半圆上选定一点![]() ,改建后的绿化区域由扇形区域
,改建后的绿化区域由扇形区域![]() 和三角形区域
和三角形区域![]() 组成,其面积为
组成,其面积为![]() ,设
,设![]()
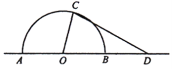
(1)写出![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ,并指出
,并指出![]() 的取值范围;
的取值范围;
(2)试问![]() 多大时,改建后的绿化区域面积
多大时,改建后的绿化区域面积![]() 最大.
最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在“普及环保知识节”后,为了进一步增强环保意识,从本校学生中随机抽取了一批学生参加环保基础知识测试.经统计,这批学生测试的分数全部介于75至100之间.将数据分成以下![]() 组:第1组
组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.

(Ⅰ)求a的值;
(Ⅱ)现采用分层抽样的方法,从第3,4,5组中随机抽取6名学生座谈,求每组抽取的学生人数;
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,试估计随机抽取学生所得测试分数的平均值在第几组(只需写出结论).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com