
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源:2015-2016学年广东中山一中高二上第二次段考数学卷(解析版) 题型:解答题
设数列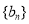 ,
, ,已知
,已知 ,
, ,
,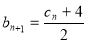 ,
, (
( ).
).
(Ⅰ)设 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅱ)求证:对任意 ,
, 为定值;
为定值;
(Ⅲ)设 为数列
为数列 的前
的前 项和,若对任意
项和,若对任意 ,都有
,都有 ,求实数
,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省抚州市高一上学期期末质量检测数学试卷(解析版) 题型:选择题
已知偶函数 满足
满足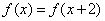 ,且当
,且当 时,
时, ,其图像与直线
,其图像与直线 在
在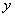 轴右侧的交点按横坐标从小到大依次记为
轴右侧的交点按横坐标从小到大依次记为 ,则
,则 等于( )
等于( )
A.2 B.4 C.8 D.16
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省高二下学期第一次月考理科数学试卷(解析版) 题型:解答题
2012年中华人民共和国环境保护部批准《环境空气质量标准》为国家环境质量标准,该标准增设和调整了颗粒物、二氧化氮、铅、笨等的浓度限值,并从2016年1月1日起在全国实施.空气质量的好坏由空气质量指数确定,空气质量指数越高,代表空气污染越严重,某市对市辖的某两个区加大了对空气质量的治理力度,从2015年11月1日起监测了100天的空气质量指数,并按照空气质量指数划分为:指标小于或等于 为通过,并引进项目投资.大于
为通过,并引进项目投资.大于 为未通过,并进行治理.现统计如下.
为未通过,并进行治理.现统计如下.
空气质量指数 |
|
|
|
|
|
|
空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
甲区天数 | 13 | 20 | 42 | 20[来源 | 3 | 2 |
乙区天数 | 8 | 32 | 40[来源 | 16 | 2 | 2 |
(Ⅰ)以频率值作为概率值,求甲区和乙区通过监测的概率;
(Ⅱ)对于甲区,若通过,引进项目可增加税收40(百万元),若没通过监测,则治理花费5(百万元);对于乙,若通过,引进项目可增加税收50(百万元),若没通过监测,则治理花费10(百万元).在(Ⅰ)的前提下,记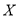 为通过监测,引进项目增加的税收总额,求随机变量
为通过监测,引进项目增加的税收总额,求随机变量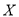 的分布列和数学期望;
的分布列和数学期望;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com