练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．求函数y=8+$\frac{2}{x}$+$\frac{1}{{x}^{2}}$的单调区间．

    分析 求导y′=-$\frac{2}{{x}^{2}}$-$\frac{2}{{x}^{3}}$=-2•$\frac{x+1}{{x}^{3}}$，从而确定导数的正负，再确定函数的单调区间．

    解答 解：∵y=8+$\frac{2}{x}$+$\frac{1}{{x}^{2}}$，
    ∴y′=-$\frac{2}{{x}^{2}}$-$\frac{2}{{x}^{3}}$=-2•$\frac{x+1}{{x}^{3}}$，
    故当x＜-1时，y′＜0，当-1＜x＜0时，y′＞0，当x＞0时，y′＜0；
    故函数y=8+$\frac{2}{x}$+$\frac{1}{{x}^{2}}$的单调减区间为（-∞，-1），（0，+∞），
    单调增区间为（-1，0）．

    点评 本题考查了导数的综合应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    6．设x、y∈R+，且满足xy+x+y=3．则x+y的最小值为2，x+2y的最小值为$4\sqrt{2}-3$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．计算：
    （1）（$\root{4}{{b}^{-\frac{2}{3}}}$）${\;}^{-\frac{2}{3}}$（b＞0）；
    （2）（0.0081）${\;}^{-\frac{1}{4}}$-[3×（$\frac{7}{8}$）0]-1•[81-0.25+（3$\frac{3}{8}$）${\;}^{-\frac{1}{3}}$]${\;}^{-\frac{1}{2}}$-10×0.027${\;}^{\frac{1}{3}}$；
    （3）$\frac{{a}^{\frac{4}{3}}-8{a}^{\frac{1}{3}}b}{4{b}^{\frac{2}{3}}+2•\root{3}{ab}+a^\frac{2}{3}}$÷（1-2•$\root{3}{\frac{b}{a}}$）×$\root{3}{ab}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知函数f（x）=lnx+$\frac{1-x}{ax}$．
    （1）若函数f（x）在（1，+∞）上为增函数，求a的取值范围；
    （2）设数列{bn}的前n项和为Sn，其中bn=$\frac{1}{n}$，求证：n≥2时，1+lnn＞Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知O是三角形ABC内部一点，满足$\overrightarrow{OA}$+2$\overrightarrow{OB}$=4$\overrightarrow{CO}$，则$\frac{{S}_{△AOB}}{{S}_{△AOC}}$=（　　）
    A．$\frac{3}{2}$B．5C．2D．$\frac{5}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

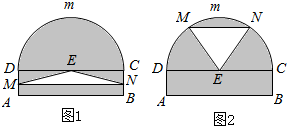    3．某仓库为了保持库内的湿度和温度，四周墙上均装有如图所示的自动通风设施．该设施的下部ABCD是矩形，其中AB=2米，BC=0.5米．上部CmD是个半圆，固定
    点E为CD的中点．△EMN是由电脑控制其形状变化的三角通风窗（阴影部分均不通风），MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆（MN和AB，CD不重合）．
    （Ⅰ）当MN和AB之间的距离为1米时，求此时三角通风窗EMN的通风面积；
    （Ⅱ）设MN与AB之间的距离为x米，试将三角通风窗EMN的通风面积S（平方米）表示成关于x的函数S=f（x）
    （Ⅲ）当MN与AB之间的距离为多少米时，三角通风窗EMN的通风面积最大？并求出这个最大面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．设a，b为不重合的两条直线，α，β为不重合的两个平面，给出下列命题：
    （1）若a∥α且b∥α，则a∥b；
    （2）如果平面α内的两条相交的直线a，b都平行于平面β，那么α∥β；
    （3）如果a，b为异面直线，那么a，b所成的角θ的范围是0＜θ＜π；
    （4）如果a，b为异面直线，那么过a，b外一点有且仅有一个平面α与a，b都平行；
    上面命题中，所有假命题的序号是（1）（3）（4）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．设x＞y＞0，则下列各式中正确的是（　　）
    A．x＞$\frac{x+y}{2}$＞$\sqrt{xy}$＞yB．y＞$\frac{x+y}{2}$＞$\sqrt{xy}$＞xC．x＞$\frac{x+y}{2}$＞y＞$\sqrt{xy}$D．y＞$\frac{x+y}{2}$≥$\sqrt{xy}$＞x

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=ax3+3x2-6ax-11，g（x）=3x2+6x+12，和直线m：y=kx+9．又f′（-1）=0．
    （1）求a的值；
    （2）如果对于所有x≥-2的x，都有f（x）≤kx+9≤g（x）成立，求k的取值范围．
    （3）是否存在k的值，使直线m既是曲线y=f（x）的切线，又是y=g（x）的切线；如果存在，求出k的值；如果不存在，说明理由．

    查看答案和解析>>

    同步练习册答案