
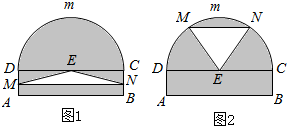
 某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定
某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定分析 (1)当MN和AB之间的距离为1米时,MN应位于DC上方,且此时△EMN中MN边上的高为0.5米,从而可求MN的长,由三角形面积公式求面积;
(2)当MN在矩形区域内滑动,即x∈(0,$\frac{1}{2}$),由三角形面积公式建立面积模型.当MN在半圆形区域内滑动,即x∈($\frac{1}{2}$,$\frac{3}{2}$)时,由三角形面积公式建立面积模型;
(3)根据分段函数,分别求得每段上的最大值,最后取它们当中最大的,即为原函数的最大值,并明确取值的状态,从而得到实际问题的建设方案.
解答 解:(1)由题意,当MN和AB之间的距离为1米时,
MN应位于DC上方,且此时△EMN中MN边上的高为0.5米,
又因为EM=EN=1米,所以MN=$\sqrt{3}$米,
所以S△EMN=$\frac{\sqrt{3}}{4}$,即三角通风窗EMN的通风面积为$\frac{\sqrt{3}}{4}$;
(2)当MN在矩形区域内滑动,即x∈(0,$\frac{1}{2}$)时,
△EMN的面积S=$\frac{1}{2}$MN•($\frac{1}{2}$-x)=$\frac{1}{2}$-x;
当MN在半圆形区域内滑动,即x∈($\frac{1}{2}$,$\frac{3}{2}$)时,
△EMN的面积S=(x-$\frac{1}{2}$)•$\sqrt{1-(x-\frac{1}{2})^{2}}$.
综上可得S=f(x)=$\left\{\begin{array}{l}{\frac{1}{2}-x,x∈(0,\frac{1}{2})}\\{(x-\frac{1}{2})•\sqrt{1-(x-\frac{1}{2})^{2}},x∈(\frac{1}{2},\frac{3}{2})}\end{array}\right.$;
(3)当MN在矩形区域内滑动时,f(x)在区间(0,$\frac{1}{2}$)上单调递减,
则f(x)<f(0)=$\frac{1}{2}$;
当MN在半圆形区域内滑动,f(x)=(x-$\frac{1}{2}$)•$\sqrt{1-(x-\frac{1}{2})^{2}}$
≤$\frac{(x-\frac{1}{2})^{2}+1-(x-\frac{1}{2})^{2}}{2}$=$\frac{1}{2}$,等号成立时,x=$\frac{1}{2}$(1+$\sqrt{2}$).
因此当x=$\frac{1}{2}$(1+$\sqrt{2}$)(米)时,每个三角形得到最大通风面积为$\frac{1}{2}$平方米.
点评 本题主要考查函数模型的建立与应用,主要涉及了三角形面积公式,分段函数求最值以及基本不等式法等解题方法.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{nd}{{a}_{1}({a}_{1}+nd)}$ | B. | $\frac{n}{{a}_{1}({a}_{1}+nd)}$ | C. | $\frac{d}{{a}_{1}({a}_{1}+nd)}$ | D. | $\frac{n+1}{{a}_{1}[{a}_{1}+(n+1)d]}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com