
| A. | $\frac{nd}{{a}_{1}({a}_{1}+nd)}$ | B. | $\frac{n}{{a}_{1}({a}_{1}+nd)}$ | C. | $\frac{d}{{a}_{1}({a}_{1}+nd)}$ | D. | $\frac{n+1}{{a}_{1}[{a}_{1}+(n+1)d]}$ |
分析 由已知条件利用等差数列的通项公式得$\frac{1}{{a}_{n}{a}_{n+1}}=\frac{1}{d}(\frac{1}{{a}_{n}}-\frac{1}{{a}_{n+1}})$,由此能求出$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{a}_{2}{a}_{3}}$+…+$\frac{1}{{a}_{n}{a}_{n+1}}$的值.
解答 解:∵等差数列公差为d,且an≠0,d≠0,
∴$\frac{1}{{a}_{n}{a}_{n+1}}=\frac{1}{d}(\frac{1}{{a}_{n}}-\frac{1}{{a}_{n+1}})$,
∴$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{a}_{2}{a}_{3}}$+…+$\frac{1}{{a}_{n}{a}_{n+1}}$
=$\frac{1}{d}(\frac{1}{{a}_{1}}-\frac{1}{{a}_{2}}+\frac{1}{{a}_{2}}-\frac{1}{{a}_{3}}+…+\frac{1}{{a}_{n}}-\frac{1}{{a}_{n+1}})$
=$\frac{1}{d}(\frac{1}{{a}_{1}}-\frac{1}{{a}_{n+1}})$
=$\frac{n}{{a}_{1}•{a}_{n+1}}$
=$\frac{n}{{a}_{1}({a}_{1}+nd)}$.
故选:B.
点评 本题考查有关等差数列的求值,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
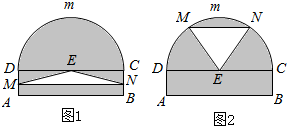 某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定
某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com