Question

已知函致f （x）=x³+bx²+cx+d．
（I）当b=0时，证明：曲线y=f（x）与其在点（0，f（0））处的切线只有一个公共点；
（Ⅱ）若曲线y=f（x）在点（1，f（1））处的切线为12x+y-13=0，记函数y=f（x）的两个极值点为x₁，x₂，当x₁+x₂=2时，求f（x₁）+f（x₂）．

Answer 1

（Ⅰ）证明：当b=0时，f（x）=x³+cx+d，f′（x）=3x²+c．
∴f（0）=d，f′（0）=c．
曲线y=f（x）与其在点（0，f（0））处的切线为y=cx+d．
由消去y，得x³=0，x=0．
所以曲线y=f（x）与其在点（0，f（0））处的切线只有一个公共点即切点．
（Ⅱ）解：由已知，切点为（1，1）．
又f′（x）=3x²+2bx+c，于是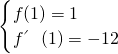，即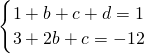得c=-2b-15，d=b+15．
从而f（x）=x³+bx²-（2b+15）x+b+15，f′（x）=3x²+2bx-2b-15．
依题设，x₁+x₂=-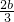，故b=-3．
于是f（x）=x³-3x²-9x+12，f′（x）=3x²-6x-9=3（x+1）（x-3）．
当x变化时，f′（x），f（x）的变化如下：

x	（-∞，-1）	-1	（-1，3）	3	（3，+∞）
f′（x）	+	0	-	0	+
f（x）	↗	极大值17	↘	极小值-15	↗

由此知，f（x₁）+f（x₂）=2．

分析：（Ⅰ）求导函数，确定切线的斜率，从而可得切线方程，与已知曲线联立，即可得到结论；
（Ⅱ）确定切点坐标，利用导数确定函数的单调性与极值，即可求得结论．
点评：本题考查导数知识的运用，考查函数的单调性与极值，考查学生的计算能力，属于中档题．