
| 黑 | 红 | |
| 男 | 17 | 9 |
| 女 | 6 | 22 |
| 54×(17×22-9×6)2 |
| 26×23×31×28 |
| 54×(17×22-9×6)2 |
| 26×23×31×28 |


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
| 成绩 | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) |
| 频数 | 4 | 20 | 15 | 10 | 1 |
| 成绩 | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) |
| 频数 | 1 | 11 | 23 | 13 | 2 |
| 成绩小于100 | 成绩不小于100分 | 合计 | |
| 甲班 | 50 | ||
| 乙班 | 50 | ||
| 合计 | 36 | 64 | 100 |
| p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 黑 | 红 | |
| 男 | 17 | 9 |
| 女 | 6 | 22 |
| 54×(17×22-9×6)2 |
| 26×23×31×28 |
查看答案和解析>>
科目:高中数学 来源: 题型:
某厂家为调查一种新推出的产品的颜色接受程度是否与性别有关,数据如下表:
| 黑 | 红 | |
| 男 | 17 | 9 |
| 女 | 6 | 22 |
根据表中的数据,得到k=![]() ≈10.653,因为K2≥7.879,所以产品的颜色接受程度与性别有关系,那么这种判断出错的可能性为 .
≈10.653,因为K2≥7.879,所以产品的颜色接受程度与性别有关系,那么这种判断出错的可能性为 .
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省广州市海珠区高二(下)期末数学试卷(文科)(解析版) 题型:填空题
| 黑 | 红 | |
| 男 | 17 | 9 |
| 女 | 6 | 22 |
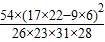 ≈10.653,因为K2≥7.879,所以产品的颜色接受程度与性别有关系,那么这种判断出错的可能性为 .
≈10.653,因为K2≥7.879,所以产品的颜色接受程度与性别有关系,那么这种判断出错的可能性为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com