
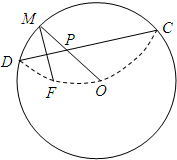
 一圆形纸片的半径为10cm,圆心为O,F为圆内一定点,OF=6cm,M为圆周上任意一点,把圆纸片折叠,使M与F重合,然后抹平纸片,这样就得到一条折痕CD,设CD与OM交于P点(如图),建立适当的直角坐标系,求点P的轨迹方程.
一圆形纸片的半径为10cm,圆心为O,F为圆内一定点,OF=6cm,M为圆周上任意一点,把圆纸片折叠,使M与F重合,然后抹平纸片,这样就得到一条折痕CD,设CD与OM交于P点(如图),建立适当的直角坐标系,求点P的轨迹方程.科目:高中数学 来源: 题型:
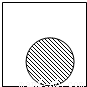
 张老师有天觉得很无聊,她把一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,那么在正方形内,这张圆形纸片“不能接触到的部分”的面积是( )
张老师有天觉得很无聊,她把一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,那么在正方形内,这张圆形纸片“不能接触到的部分”的面积是( )查看答案和解析>>
科目:高中数学 来源:广东省培正中学2011-2012学年高二第一学期期中考考试数学理科试题 题型:044
一圆形纸片的半径为10 cm,圆心为O,F为圆内一定点,OF=6 cm,M为圆周上任意一点,把圆纸片折叠,使M与F重合,然后抹平纸片,这样就得到一条折痕CD,设CD与OM交于P点,如图

(1)求点P的轨迹方程;
(2)求证:直线CD为点P轨迹的切线.
查看答案和解析>>
科目:高中数学 来源: 题型:
一圆形纸片的半径为10cm,圆心为O,F为圆内一定点,OF=6cm,M为圆周上任意一点,把圆纸片折叠,使M与F重合,然后抹平纸片,这样就得到一条折痕CD,设CD与OM交于P点,如图
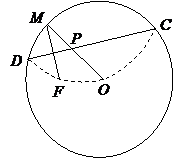
(1)求点P的轨迹方程;
(2)求证:直线CD为点P轨迹的切线.
查看答案和解析>>
科目:高中数学 来源:2011-2012年广东省高二上学期期中考试理科数学 题型:解答题
(本小题满分14分) 一圆形纸片的半径为10cm,圆心为O,
F为圆内一定点,OF=6cm,M为圆周上任意一点,把圆纸片折叠,
使M与F重合,然后抹平纸片,这样就得到一条折痕CD,设CD
与OM交于P点,如图
(1)求点P的轨迹方程;
(2)求证:直线CD为点P轨迹的切线.

查看答案和解析>>
科目:高中数学 来源:2012-2013学年重庆94中高三(上)第五次月考数学试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com