练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

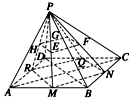
    已知ABCD是平行四边形，P点是ABCD所在平面外的一点，连接PA、PB、PC、PD.设点E、F、G、H分别为△PAB、△PBC、△PCD、△PDA的重心.

    （1）试用向量方法证明E、F、G、H四点共面；

    （2）试判断平面EFGH与平面ABCD的位置关系，并用向量方法证明你的判断.

    (1)证明略(2) 平面EFGH∥平面ABCD


    解析:

    （1）  分别延长PE、PF、PG、PH交对边于M、N、Q、R点，因为E、F、G、H分别是所在三角形的重心，所以M、N、Q、R为所在边的中点，顺次连接M、N、Q、R得到的四边形为平行四边形，且有=，

    =，=， =

    ∴=+

    =（-）+（-）

    =（-）+（-）

    =（+）

    又∵=-=-=

    ∴=（+）,∴=+

    由共面向量定理知：E、F、G、H四点共面.

    (2)  由（1）得=,故∥.

    又∵平面ABC，EG平面ABC.

    ∴EG∥平面ABC.

    又∵=-=-=

    ∴MN∥EF，又∵MN平面ABC，EF平面ABC，

    EF∥平面ABC.

    ∵EG与EF交于E点，

    ∴平面EFGH∥平面ABCD.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    9、如图，已知四边形ABCD是平行四边形，点P是平面ABCD外的一点，则在四棱锥P-ABCD中，M是PC的中点，在DM上取一点G，过G和AP作平面交平面BDM于GH．
    求证：AP∥GH．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

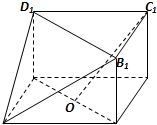    如图，在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中，已知BB1⊥平面BCD，四边形ABCD是平行四边形，∠ABC=120°，AB=2，AD=4，BB1=1．
    设O是线段BD的中点．
    （1）求证：C1O∥平面AB1D1；
    （2）证明：平面AB1D1⊥平面ADD1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•杭州二模）如图，已知在四棱锥P-ABCD中，底面ABCD是平行四边形，PA⊥平面ABCD，PA=
    		3
    ，AB=1．AD=2．∠BAD=120°，E，F，G，H分别是BC，PB，PC，AD的中点．
    （Ⅰ）求证：PH∥平面GED；
    （Ⅱ）过点F作平面α，使ED∥平面α，当平面α⊥平面EDG时，设PA与平面α交于点Q，求PQ的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知四棱锥V-ABCD，底面ABCD是平行四边形，点V在平面ABCD上的射影E在AD边上，且AE=
    1
    3
    ED    ，VE=4，BE=EC=2，∠BEC=90°．
    （Ⅰ）设F是BC的中点，求异面直线EF与VC所成角的余弦值；
    （Ⅱ）设点P在棱VC上，且DP⊥EC．求
    VP
    PC
    的值．

    查看答案和解析>>

    科目：高中数学 来源：设计必修四数学北师版 北师版 题型：013

    已知M是平行四边形ABCD对角线的交点，下列四式中不能化简为的是

    [　　]

    A．

    B．

    C．

    D．

    查看答案和解析>>

    同步练习册答案