
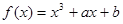 的图象是曲线C,直线
的图象是曲线C,直线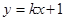 与曲线
与曲线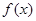 的解析式;
的解析式;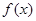 的递增区间;
的递增区间;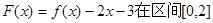 上的最大值和最小值.
上的最大值和最小值.科目:高中数学 来源:不详 题型:解答题
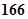 千米.假设某汽车从上海莘庄镇进入该高速公路后以不低于
千米.假设某汽车从上海莘庄镇进入该高速公路后以不低于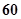 千米/时且不高于
千米/时且不高于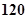 千米/时的时速匀速行驶到杭州.已知该汽车每小时的运输成本
千米/时的时速匀速行驶到杭州.已知该汽车每小时的运输成本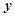 (以元为单位)由可变部分和固定部分组成:可变部分与速度
(以元为单位)由可变部分和固定部分组成:可变部分与速度 (千米/时)的平方成正比,比例系数为
(千米/时)的平方成正比,比例系数为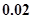 ;固定部分为200元.
;固定部分为200元.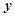 (元)表示为速度
(元)表示为速度 (千米/时)的函数,并指出这个函数的定义域;
(千米/时)的函数,并指出这个函数的定义域;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
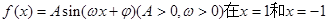 处分别取得最大值和最小值,且对于任意
处分别取得最大值和最小值,且对于任意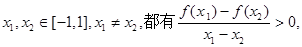 则
则A.函数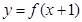 一定是周期为4的偶函数 一定是周期为4的偶函数 |
B.函数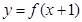 一定是周期为2的奇函数 一定是周期为2的奇函数 |
C.函数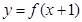 一定是周期为4的奇函数 一定是周期为4的奇函数 |
D.函数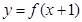 一定是周期为2的偶函数 一定是周期为2的偶函数 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ;⑤y=cosx.其中为一阶格点函数的是________(填序号).
;⑤y=cosx.其中为一阶格点函数的是________(填序号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com