
【题目】已知函数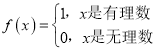 ,则下列判断中是真命题的有( ).
,则下列判断中是真命题的有( ).
①![]() ,
,![]() ;②
;②![]() 是偶函数;③对于任意一个非零有理数
是偶函数;③对于任意一个非零有理数![]() ,
,![]() ,
,![]() ;④存在三个点
;④存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等边三角形.
为等边三角形.
A.①②③B.①②③④C.①③④D.②③④
【答案】B
【解析】
①根据函数的对应法则,可知无论x是有理数还是无理数,均有f(f(x))=1;
②根据函数奇偶性的定义,可得f(x)是偶函数;
③根据函数的表达式,结合有理数和无理数的性质;
④取x1=![]() ,x2=0,x3=
,x2=0,x3=![]() ,可得
,可得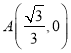 ,
,![]() ,
,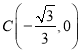 ,三点恰好构成等边三角形.
,三点恰好构成等边三角形.
①∵当x为有理数时,f(x)=1;当x为无理数时,f(x)=0,
∴当x为有理数时,![]() =f(1)=1;当x为无理数时,
=f(1)=1;当x为无理数时,![]() =f(0)=1,
=f(0)=1,
即无论x是有理数还是无理数,均有![]() =1,故①正确;
=1,故①正确;
②∵有理数的相反数还是有理数,无理数的相反数还是无理数,
∴对任意x∈R,都有![]() ,故②正确;
,故②正确;
③若x是有理数,则x+T也是有理数; 若x是无理数,则x+T也是无理数,
∴根据函数的表达式,任取一个不为零的有理数T,![]() 对x∈R恒成立,故③正确;
对x∈R恒成立,故③正确;
④取x1=![]() ,x2=0,x3=
,x2=0,x3=![]() ,可得
,可得![]() ,
,
∴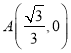 ,
,![]() ,
,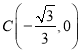 ,恰好△ABC为等边三角形,故④正确.
,恰好△ABC为等边三角形,故④正确.
即真命题的个数是4个,
故选:B.


科目:高中数学 来源: 题型:
【题目】在极坐标系中,过曲线![]() 外的一点
外的一点![]() (其中
(其中![]() ,
,![]() 为锐角)作平行于
为锐角)作平行于![]() 的直线
的直线![]() 与曲线分别交于
与曲线分别交于![]() .
.
(Ⅰ) 写出曲线![]() 和直线
和直线![]() 的普通方程(以极点为原点,极轴为
的普通方程(以极点为原点,极轴为![]() 轴的正半轴建系);
轴的正半轴建系);
(Ⅱ)若![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.

(1)证明:AE⊥PD;
(2)若AB=2,PA=2,求二面角E-AF-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设D是圆O:x2+y2=16上的任意一点,m是过点D且与x轴垂直的直线,E是直线m与x轴的交点,点Q在直线m上,且满足2|EQ|![]() |ED|.当点D在圆O上运动时,记点Q的轨迹为曲线C.
|ED|.当点D在圆O上运动时,记点Q的轨迹为曲线C.
(1)求曲线C的方程.
(2)已知点P(2,3),过F(2,0)的直线l交曲线C于A,B两点,交直线x=8于点M.判定直线PA,PM,PB的斜率是否依次构成等差数列?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国新冠肺炎疫情进入常态化,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确的是( )
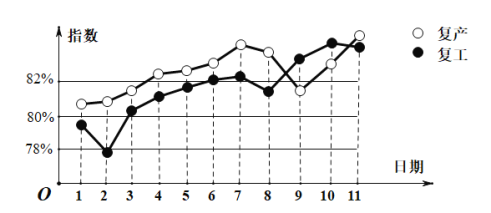
A.这11天复工指数和复产指数均逐日增加;
B.这11天期间,复产指数增量大于复工指数的增量;
C.第3天至第11天复工复产指数均超过80%;
D.第9天至第11天复产指数增量大于复工指数的增量;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构几年前对全国互联网行业进行调查统计,得到整个互联网行业从业人员年龄分布扇形图、90后从事互联网行业岗位分布条形图,则下列结论中不一定正确的是( ).
注:90后指1990-1999年之间出生的人群,80后指1980-1989年之间出生的人群,80前指179年及以前出生的人群.
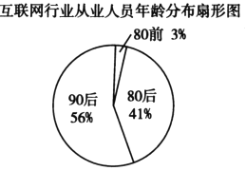

A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com