
【题目】已知点F1 , F2是椭圆C: ![]() =1的焦点,点M在椭圆C上且满足|
=1的焦点,点M在椭圆C上且满足| ![]() +
+ ![]() |=2
|=2 ![]() ,则△MF1F2的面积为( )
,则△MF1F2的面积为( )
A.![]()
B.![]()
C.1
D.2
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=﹣2,an+1=2an+4.
(1)证明数列{an+4}是等比数列并求出{an}通项公式;
(2)若 ![]() ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有学生2000人,其中高二学生630人,高三学生720人.为了解学生的身体素质情况,采用按年级分层抽样的方法,从该校学生中抽取一个200人的样本.则样本中高一学生的人数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在边长为24的正方形![]() 中,点
中,点![]() 在边
在边![]() 上,且
上,且![]() ,
, ![]() ,作
,作![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() ,作
,作![]() 分别交
分别交![]() 于点
于点![]() ,将该正方形沿
,将该正方形沿![]() 折叠,使得
折叠,使得![]() 与
与![]() 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求多面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直棱柱ABC﹣A1B1C1中,AC=BC=CC1= ![]() AB,E是线段CC1的中点,连接AE,B1E,AB1 , B1C,BC1 , 得到的图形如图所示. (Ⅰ)证明BC1⊥平面AB1C;
AB,E是线段CC1的中点,连接AE,B1E,AB1 , B1C,BC1 , 得到的图形如图所示. (Ⅰ)证明BC1⊥平面AB1C;
(Ⅱ)求二面角E﹣AB1﹣C的大小.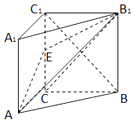
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C为△ABC的内角,tanA,tanB是关于方程x2+ ![]() px﹣p+1=0(p∈R)两个实根. (Ⅰ)求C的大小
px﹣p+1=0(p∈R)两个实根. (Ⅰ)求C的大小
(Ⅱ)若AB=3,AC= ![]() ,求p的值.
,求p的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]()
(1)求函数f(x)的最小正周期和最大值,并求出x为何值时,f(x)取得最大值;
(2)求函数f(x)在[﹣2π,2π]上的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某大风车的半径为2m,每6s旋转一周,它的最低点O离地面0.5 m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m),则函数h=f(t)的关系式( )
A.y=﹣2cos![]() +2.5
+2.5
B.y=﹣2sin![]() +2.5
+2.5
C.y=﹣2cos![]() +2.5
+2.5
D.y=﹣2sin![]() +2.5
+2.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人射击一次命中7~10环的概率如下表
命中环数 | 7 | 8 | 9 | 10 |
命中概率 | 0.16 | 0.19 | 0.28 | 0.24 |
计算这名射手在一次射击中:
(1)射中10环或9环的概率;
(2)至少射中7环的概率;
(3)射中环数不足8环的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com