
【题目】如图,在侧棱垂直于底面的三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 为侧面
为侧面![]() 的对角线的交点,
的对角线的交点,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 中点
中点
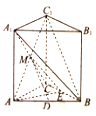
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】下列推理不属于合情推理的是( )
A. 由铜、铁、铝、金、银等金属能导电,得出一切金属都能导电.
B. 半径为![]() 的圆面积
的圆面积![]() ,则单位圆面积为
,则单位圆面积为![]() .
.
C. 由平面三角形的性质推测空间三棱锥的性质.
D. 猜想数列2,4,8,…的通项公式为![]() .
. ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某省高三男生身高情况,现从某校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组![]() ,第二组
,第二组![]() ,…,第六组
,…,第六组![]() ,下图是按照上述分组方法得到的频率分布直方图.
,下图是按照上述分组方法得到的频率分布直方图.
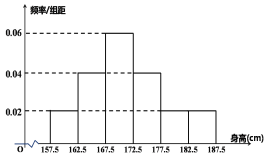
(1)求该学校高三年级男生的平均身高;
(2)利用分层抽样的方式从这50名男生中抽出20人,求抽出的这20人中,身高在177.5cm以上(含177.5cm)的人数;
(3)从根据(2)选出的身高在177.5cm以上(含177.5cm)的男生中任意抽取2人,求此二人来自于不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三条直线![]() :
:![]() (
(![]() ),
),![]() :
:![]() ,
,![]() :
:![]() ,若
,若![]() 与
与![]() 的距离是
的距离是![]() .
.
(1)求a的值:
(2)能否找到一点P,使得点P同时满足下列三个条件:①P是第一象限的点;②点P到![]() 的距离是点P到
的距离是点P到![]() 的距离的
的距离的![]() ;③点P到
;③点P到![]() 的距离与点P到
的距离与点P到![]() 的距离之比是
的距离之比是![]() ,若能,求出点P的坐标,若不能,请说明理由.
,若能,求出点P的坐标,若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,如果动点
中,如果动点![]() 在线段
在线段![]() 上,动点
上,动点![]() 在正方体
在正方体![]() 的四条边上,那么,对于任何一条直线
的四条边上,那么,对于任何一条直线![]() ,在平面
,在平面![]() 上,总存在相应的一条直线,使得该直线与直线
上,总存在相应的一条直线,使得该直线与直线![]() ( )
( )
A.平行B.异面C.相交D.垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公历![]() 月
月![]() 日为我国传统清明节,清明节扫墓我们都要献鲜花,某种鲜花的价格会随着需求量的增加而上升.一个批发市场向某地商店供应这种鲜花,具体价格统计如下表所示
日为我国传统清明节,清明节扫墓我们都要献鲜花,某种鲜花的价格会随着需求量的增加而上升.一个批发市场向某地商店供应这种鲜花,具体价格统计如下表所示
日供应量 |
|
|
|
|
|
|
单位 |
|
|
|
|
|
|
(I)根据上表中的数据进行判断,函数模型![]() 与
与![]() 哪一个更适合于体现日供应量
哪一个更适合于体现日供应量![]() 与单价
与单价![]() 之间的关系;(给出判断即可,不必说明理由)
之间的关系;(给出判断即可,不必说明理由)
(II)根据(I)的判断结果以及参考数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(III)该地区有![]() 个商店,其中
个商店,其中![]() 个商店每日对这种鲜花的需求量在
个商店每日对这种鲜花的需求量在![]() 束以下,
束以下,![]() 个商店每日对这种鲜花的需求量在
个商店每日对这种鲜花的需求量在![]() 束以上,则从这
束以上,则从这![]() 个商店个中任取
个商店个中任取![]() 个进行调查,求恰有
个进行调查,求恰有![]() 个商店对这种鲜花的需求量在
个商店对这种鲜花的需求量在![]() 束以上的概率.
束以上的概率.
参考公式及相关数据:对于一组数据![]() ,
,![]() ,...,
,...,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为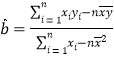 ,
,![]() .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P—ABC中,PA=3,PB=PC=![]() ,AB=AC=2,BC=
,AB=AC=2,BC=![]() .
.
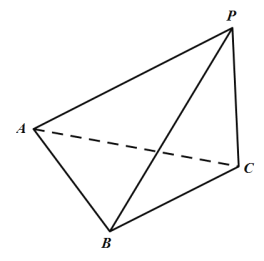
(1)求二面角B—AP—C大小的余弦值;
(2)求点P到底面ABC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面ABCD为菱形,
中,底面ABCD为菱形,![]() ,侧面
,侧面![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() ,点E为棱AD的中点.
,点E为棱AD的中点.
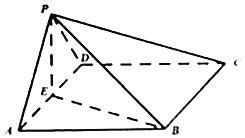
(1)求证:![]() 平面ABCD;
平面ABCD;
(2)求直线AB与平面PBC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com