练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如下图所示,教室的墙壁上挂着一块黑板,它的上、下边缘分别在学生水平视线上方a m和b m,问学生距离多远时看黑板的视角最大?

    解:设点P处距黑板x m远,∠APH=α,∠BPH=β,则tanα=,tanβ=.

    ∴tan(α-β)===(x＞0).

        由函数单调性知x+≥2,

        当x=时,tan(α-β)最大,

        又α-β为锐角,所以x=时,学生看黑板的视角α-β最大.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：013

    平面区域如下图所示表示的不等式是

    [　　]

    A．2x＋y－4＜0
    B．2x＋y－4≤0
    C．2x＋y－4＞0
    D．2x＋y－4≥0

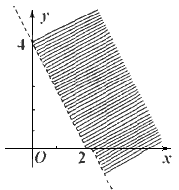
    查看答案和解析>>

    科目：高中数学 来源：101网校同步练习　高二数学　苏教版(新课标·2004年初审) 苏教版 题型：013

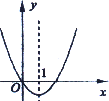
    二次函数f(x)的图象如下图所示，的图象在下面选项中，则这个图象是

    [　　]

    A．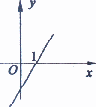

    B．

    C．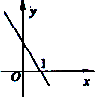

    D．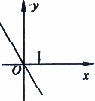

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    国家卫生部信息统计中心根据国务院新闻办公室授权发布的全国内地5月21日至5月25日非典型肺炎发病情况，按年龄段进行统计分析中，各年龄段发病的总人数如下图所示(发病的病人年龄在0～80岁之间)，请你观察图形回答下面的问题．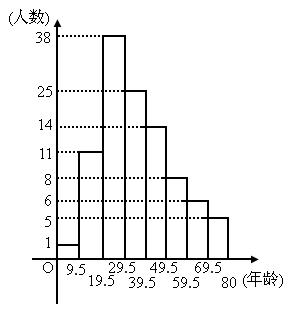

    (1)全国内地5月21日至5月25日平均每天有多少人患非典型肺炎？

    (2)年龄在29.5～39.5这一组的频数是多少？频率是多少？

    (3)根据统计图，年龄在多少岁范围内的人发病最多？

    查看答案和解析>>

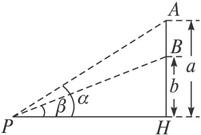
    科目：高中数学 来源： 题型：

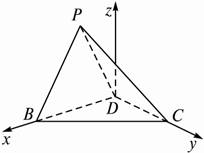
    已知在四边形ABCD中，AD∥BC，AD=AB=1，∠BCD=45°,∠BAD=90°,将△ABD沿对角线BD折起到如下图所示PBD的位置，使平面PBD⊥平面BCD.

    (1)求证：CD⊥PB；

    （2）求二面角P—BC—D的大小（用反三角函数表示）；

    （3）求点D到平面PBC的距离.

    查看答案和解析>>

    同步练习册答案