练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    我们常用构造等式对同一个量算两次的方法来证明组合恒等式，如由等式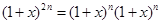可得，左边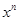的系数为，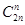

    而右边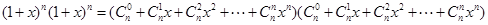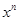， 的系数为，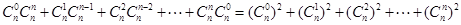

    由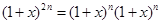恒成立，可得．

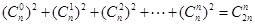    利用上述方法，化简      ．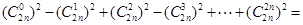

     

    【答案】

    【解析】

    试题分析：构造等式（x-1）2n?（x+1）2n=（x2-1）2n，由左式可得x2n的系数为C2n2n?（-1）2nC2n0+C2n2n-1?（-1）2n-1C2n1+C2n2n-2?（-1）2n-2C2n2+…+C2n0?（-1）0C2n2n，即（C2n0）2-（C2n1）2+（C2n2）2-（C2n3）2+…+（C2n2n）2，由右式可得得x2n的系数为（-1）nC2nn，故有（C2n0）2-（C2n1）2+（C2n2）2-（C2n3）2+…+（C2n2n）2=（-1）nC2nn，

    考点：本题考查了组合数的运用

    点评：对于此类组合数的应用问题，常常涉及二项式定理的应用，关键要根据题意，充分利用组合数的性质．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （Ⅰ）求证：
    C
    m
    n
    =
    n
    m
    C
    m-1
    n-1
    ；
    （Ⅱ）利用第（Ⅰ）问的结果证明Cn1+2Cn2+3Cn3+…+nCnn=n•2n-1；  
    （Ⅲ）其实我们常借用构造等式，对同一个量算两次的方法来证明组合等式，譬如：（1+x）1+（1+x）2+（1+x）3+…+（1+x）n=
    (1+x)[1-(1+x)n]
    1-(1+x)
    =
    (1+x)n+1-(1+x)
    x
    ；，由左边可求得x2的系数为C22+C32+C42+…+Cn2，利用右式可得x2的系数为Cn+13，所以C22+C32+C42+…+Cn2=Cn+13．请利用此方法证明：（C2n0）2-（C2n1）2+（C2n2）2-（C2n3）2+…+（C2n2n）2=（-1）nC2nn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    我们常用构造等式对同一个量算两次的方法来证明组合恒等式，如由等式（1+x）2n=（1+x）n（1+x）n可得，左边xn的系数为
    C
    n
    2n
    ，而右边(1+x)n(1+x)n=(
    C
    0
    n
    +
    C
    1
    n
    x+
    C
    2
    n
    x2+…+
    C
    n
    n
    xn)(
    C
    0
    n
    +
    C
    1
    n
    x+
    C
    2
    n
    x2+…+
    C
    n
    n
    xn)    ，xn的系数为
    C
    0
    n
    C
    n
    n
    +
    C
    1
    n
    C
    n-1
    n
    +
    C
    2
    n
    C
    n-2
    n
    +…+
    C
    n
    n
    C
    0
    n
    =(
    C
    0
    n
    )2+(
    C
    1
    n
    )2+(
    C
    2
    n
    )2+…+(
    C
    n
    n
    )2    ，由（1+x）2n=（1+x）n（1+x）n恒成立，可得(
    C
    0
    n
    )2+(
    C
    1
    n
    )2+(
    C
    2
    n
    )2+…+(
    C
    n
    n
    )2=
    C
    n
    2n
    ．
    利用上述方法，化简(
    C
    0
    2n
    )2-(
    C
    1
    2n
    )2+(
    C
    2
    2n
    )2-(
    C
    3
    2n
    )2+…+(
    C
    2n
    2n
    )2    =
    (-1)n
    C
    n
    2n
    (-1)n
    C
    n
    2n
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    我们知道，对一个量用两种方法分别算一次，由结果相同可以构造等式，这是一种非常有用的思想方法--“算两次”（G．Fubini原理），如小学有列方程解应用题，中学有等积法求高…
    请结合二项式定理，利用等式（1+x）n•（1+x）n=（1+x）2n（n∈N*）
    证明：
    （1）
    n
    r=0
    (
    C
    r
    n
    )2=
    C
    n
    2n
    ；  
    （2）
    m
    r=0
    (
    C
    r
    n
    C
    m-r
    n
    )=
    C
    m
    2n
    ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    我们常用构造等式对同一个量算两次的方法来证明组合恒等式，如由等式（1+x）2n=（1+x）n（1+x）n可得，左边xn的系数为
    Cn2n
    ，而右边(1+x)n(1+x)n=(
    C0n
    +
    C1n
    x+
    C2n
    x2+…+
    Cnn
    xn)(
    C0n
    +
    C1n
    x+
    C2n
    x2+…+
    Cnn
    xn)    ，xn的系数为
    C0n
    Cnn
    +
    C1n
    Cn-1n
    +
    C2n
    Cn-2n
    +…+
    Cnn
    C0n
    =(
    C0n
    )2+(
    C1n
    )2+(
    C2n
    )2+…+(
    Cnn
    )2    ，由（1+x）2n=（1+x）n（1+x）n恒成立，可得(
    C0n
    )2+(
    C1n
    )2+(
    C2n
    )2+…+(
    Cnn
    )2=
    Cn2n
    ．
    利用上述方法，化简(
    C02n
    )2-(
    C12n
    )2+(
    C22n
    )2-(
    C32n
    )2+…+(
    C2n2n
    )2    =______．

    查看答案和解析>>

    同步练习册答案