
【题目】已知圆C:![]() ,点
,点![]() ,过点M且垂直于CM的直线交圆C于A,B两点,过A,B两点分别作圆C的切线,两切线相交于点P,则过点P且平行于AB的直线方程为______.
,过点M且垂直于CM的直线交圆C于A,B两点,过A,B两点分别作圆C的切线,两切线相交于点P,则过点P且平行于AB的直线方程为______.
【答案】![]()
【解析】
根据题意,由圆的标准方程分析可得圆心坐标和半径,计算可得直线CM、AB的斜率,即可得直线AB的方程,设要求直线为l,其方程为x+y﹣m=0,分析可得Rt△CAM~Rt△CPA,则有![]() =
=![]() ,计算可得CP的值,分析可得直线l:x+y﹣m=0在点C的上方,且C到直线l的距离为CP=
,计算可得CP的值,分析可得直线l:x+y﹣m=0在点C的上方,且C到直线l的距离为CP=![]() ,由点到直线的距离公式可得CP=
,由点到直线的距离公式可得CP=![]() =
=![]() ,解可得m的值,将m的值代入直线x+y﹣m=0中即可得答案.
,解可得m的值,将m的值代入直线x+y﹣m=0中即可得答案.
根据题意,圆C:(x﹣1)2+(y﹣2)2=5,则圆心C(1,2),半径为![]() ,
,
则CM的斜率k=![]() =1,
=1,
则AB的斜率k=﹣1,
则AB的方程为y﹣3=﹣(x﹣2),即x+y﹣5=0,
设要求直线,过点P且平行于AB的直线为l,其方程为x+y﹣m=0,
Rt△CAM 中,CA=![]() ,CM=
,CM=![]() =
=![]() ,
,
又由Rt△CAM~Rt△CPA,
则有![]() =
=![]() ,
,
则有CP=![]() =
=![]() ,
,
直线l:x+y﹣m=0在点C的上方,且C到直线l的距离为CP=![]() ,
,
则有CP=![]() =
=![]() ,
,
解可得:m=8或m=﹣2,
又由直线l在C的上方,则m=8;
故直线l的方程为x+y﹣8=0;
故答案为:x+y﹣8=0.


科目:高中数学 来源: 题型:
【题目】已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.现给出如下结论:
①f(0)f(1)>0; ②f(0)f(1)<0;
③f(0)f(3)>0; ④f(0)f(3)<0.
其中正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人各射击一次,击中目标的概率分别是 ![]() 和
和 ![]() .假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
.假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
(1)求甲射击4次,至少1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(3)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
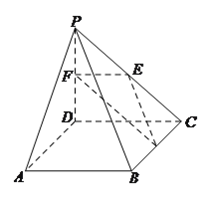
【题目】如图,在四棱锥![]() 中,
中, ![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() ,
, ![]() 的中点.
的中点.
(![]() )求四棱锥
)求四棱锥![]() 的体积.
的体积.
(![]() )求证:平面
)求证:平面![]() 平面
平面![]() .
.
(![]() )在线段
)在线段![]() 上确定一点
上确定一点![]() ,使
,使![]() 平面
平面![]() ,并给出证明.
,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲,乙两个靶,某射手向甲靶射击一次,命中的概率是 ![]() ,向乙靶射击两次,每次命中的概率是
,向乙靶射击两次,每次命中的概率是 ![]() ,若该射手每次射击的结果相互独立,则该射手完成以上三次射击恰好命中一次的概率是( )
,若该射手每次射击的结果相互独立,则该射手完成以上三次射击恰好命中一次的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图所示.

(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为[220,240),[240,260),[260,280),[280,300]的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 某人打靶,射击10次,击中7次,那么此人中靶的概率为0.7
B. 一位同学做掷硬币试验,掷6次,一定有3次“正面朝上”
C. 某地发行福利彩票,回报率为![]() ,有人花了100元钱买彩票,一定会有47元的回报
,有人花了100元钱买彩票,一定会有47元的回报
D. 概率等于1的事件不一定为必然事件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com