
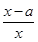 (a≠0).
(a≠0).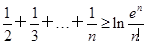 (e为自然对数的底数);
(e为自然对数的底数);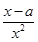 .
.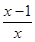 ≥f(1)=0,故
≥f(1)=0,故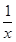 ≥1-ln x=ln
≥1-ln x=ln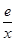 ,
,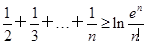 .
.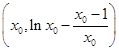 ,∴切线方程为y+1=
,∴切线方程为y+1=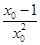 (x-1),将点T坐标代入得ln x0-
(x-1),将点T坐标代入得ln x0-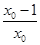 +1=
+1=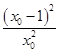 ,即ln x0+
,即ln x0+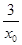 -
-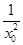 -1=0,①
-1=0,①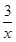 -
-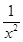 -1,则g′(x)=
-1,则g′(x)=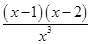 .
.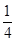 >0.
>0.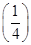 =ln
=ln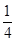 +12-16-1=-ln 4-5<0.
+12-16-1=-ln 4-5<0.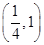 内有且仅有一根,方程①有且仅有一解,故符合条件的切线仅有一条.
内有且仅有一根,方程①有且仅有一解,故符合条件的切线仅有一条.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:不详 题型:解答题
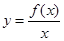 在
在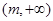 上为增函数(
上为增函数( 为常数),则称
为常数),则称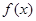 为区间
为区间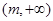 上的“一阶比增函数”,
上的“一阶比增函数”,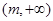 为
为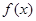 的一阶比增区间.
的一阶比增区间.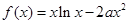 是
是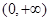 上的“一阶比增函数”,求实数
上的“一阶比增函数”,求实数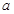 的取值范围;
的取值范围;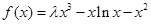 (
(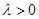 ,
,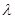 为常数),且
为常数),且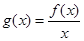 有唯一的零点,求
有唯一的零点,求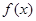 的“一阶比增区间”;
的“一阶比增区间”; 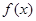 是
是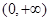 上的“一阶比增函数”,求证:
上的“一阶比增函数”,求证: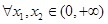 ,
,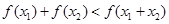
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
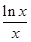 +
+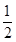 是否有实数解,并说明理由.
是否有实数解,并说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
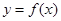 的导数
的导数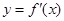 的图像,下列四个结论:
的图像,下列四个结论: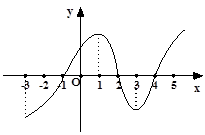
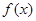 在区间
在区间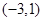 上是增函数;
上是增函数; 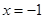 是
是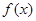 的极小值点;
的极小值点;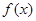 在区间
在区间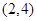 上是减函数,在区间
上是减函数,在区间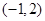 上是增函数;
上是增函数;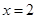 是
是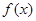 的极小值点.其中正确的结论是
的极小值点.其中正确的结论是| A.①②③ |
| B.②③ |
| C.③④ |
| D.①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com