
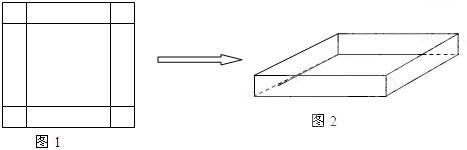
有一块边长为4米的正方形钢板,现对其进行切割,焊接成一个长方体无盖容器(切、焊损耗忽略不计),有人用数学知识作了如下设计:在钢板的四个角处各切去一个小正方形,剩余部分围成长方体。
(Ⅰ)求这种切割、焊接而成的长方体的最大容积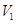 .
.
(Ⅱ)请问:能重新设计,使所得长方体的容器的容积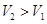 吗?若能、给出你的一种设计方案。
吗?若能、给出你的一种设计方案。
(Ⅰ)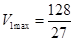 (m3);(Ⅱ)能(参考解析)
(m3);(Ⅱ)能(参考解析)
【解析】
试题分析:(Ⅰ)根据题意可得假设每个小正方形的边长为x.则通过折叠可得一个无盖的正方体.所以可以求出正方体的体积的表达.通过求导可求得体积的最大值.
(Ⅱ)本小题的设计较困难.通过对比和体积公式的应用可以假设出较多的方案.本小题的设计方案具有一定的技巧性.
试题解析:(1)设切去的小正方形边长为x.则 .所以
.所以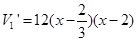 .所以当
.所以当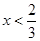 时.
时. 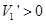 .当
.当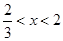 时.
时. 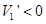 .所以当
.所以当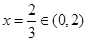 时.
时. 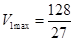 (m3).
(m3).
(2)能.如图所示.先在在正方形一边的两个角出各切下一个边长为1米的小正方形.再将这两个小正方形焊接在另一边的中间.然后焊接成长方形容器.此时. 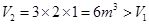 .
.
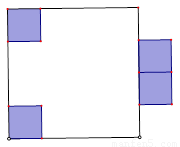
考点:1.正方体的体积的求法.2.导数求最值.3.创新思维的构造.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011年福建省莆田市高三质量检查数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com