
分析 (1)设抛物线C2:y2=2px(p≠0),则点(3,-2$\sqrt{3}$)代入,可得p=2;设椭圆方程为mx2+ny2=1,利用椭圆C1过点(-2,0),($\sqrt{2}$,$\frac{\sqrt{2}}{2}$),求出m,n,可得椭圆方程.
(2)容易验证直线l的斜率不存在时,不满足题意;当直线l斜率存在时,假设存在直线l过抛物线焦点F(1,0),设其方程为y=k(x-1),与C1的交点坐标为M(x1,y1),N(x2,y2),由y=k(x-1)代入椭圆方程消掉y,得(1+4k2)x2-8k2x+4(k2-1)=0,再由韦达定理能够导出存在直线l满足条件,且l的方程为:y=2x-2或y=-2x+2.
解答 解:(1)设抛物线C2:y2=2px(p≠0),则点(3,-2$\sqrt{3}$)代入,可得p=2,
∴C2:y2=4x;
设椭圆方程为mx2+ny2=1,
∵椭圆C1过点(-2,0),($\sqrt{2}$,$\frac{\sqrt{2}}{2}$),
∴4m=1,2m+$\frac{1}{2}$n=1,
∴m=$\frac{1}{4}$,n=1,
∴椭圆方程为$\frac{1}{4}$x2+y2=1;
(2)容易验证直线l的斜率不存在时,不满足题意;
当直线l斜率存在时,假设存在直线l过抛物线焦点F(1,0),
设其方程为y=k(x-1),与C1的交点坐标为M(x1,y1),N(x2,y2)
由y=k(x-1)代入椭圆方程,消掉y,得(1+4k2)x2-8k2x+4(k2-1)=0,
于是x1+x2=$\frac{8{k}^{2}}{1+4{k}^{2}}$,x1x2=$\frac{4({k}^{2}-1)}{1+4{k}^{2}}$
y1y2=k(x1-1)×k(x1-1)=k2[x1x2-(x1+x2)+1]=-$\frac{3{k}^{2}}{1+4{k}^{2}}$②
由$\overrightarrow{OM}⊥\overrightarrow{ON}$,得x1x2+y1y2=0(*),
将①、②代入(*)式,得$\frac{4({k}^{2}-1)}{1+4{k}^{2}}$-$\frac{3{k}^{2}}{1+4{k}^{2}}$=0
解得k=±2;
所以存在直线l满足条件,且l的方程为:y=2x-2或y=-2x+2.
点评 本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与抛物线的相关知识,解题时要注意合理地进行等价转化.


科目:高中数学 来源: 题型:解答题
| 性别 对游戏态度 | 男生 | 女生 | 合计 |
| 喜欢玩电脑游戏 | 20 | 5 | 25 |
| 不喜欢玩电脑游戏 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
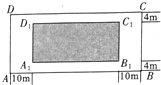 随着我市九龙江南岸江滨路建设的持续推进,未来市民将新增又一休闲好去处,据悉南江滨路建设工程规划配套建造一个长方形公园ABCD,如图所示,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成,已知休闲区A1B1C1D1的面积为4000m2,人行道的宽度分别为4m和10m.
随着我市九龙江南岸江滨路建设的持续推进,未来市民将新增又一休闲好去处,据悉南江滨路建设工程规划配套建造一个长方形公园ABCD,如图所示,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成,已知休闲区A1B1C1D1的面积为4000m2,人行道的宽度分别为4m和10m.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
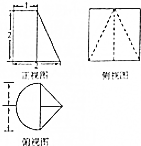
| A. | 3π+$\frac{9}{2}$ | B. | 3π+6 | C. | 5π+$\frac{9}{2}$ | D. | 5π+6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com