
| 性别 对游戏态度 | 男生 | 女生 | 合计 |
| 喜欢玩电脑游戏 | 20 | 5 | 25 |
| 不喜欢玩电脑游戏 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
分析 (1)根据所给的数据,画出列联表;
(2)根据列联表中的数据,代入求观测值的公式,求出观测值,把观测值同临界值进行比较,看到在犯错误的概率不超过0.005的前提下认为“喜欢玩电脑游戏与性别关系”.
解答 解:(1)2×2列联表
| 性别 游戏态度 | 男生 | 女生 | 总计 |
| 喜欢玩电脑游戏 | 20 | 5 | 25 |
| 不喜欢玩电脑游戏 | 10 | 15 | 25 |
| 总计 | 30 | 20 | 50 |
点评 本题考查独立性检验的应用,解题的关键是正确求出这组数据的观测值,数字运算的过程中数字比较多,不要出错.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
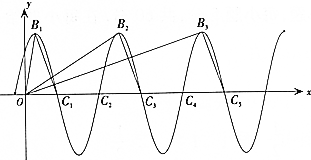 如图,已知函数f(x)=msin($\frac{π}{2}$x+$\frac{π}{4}$)(m>0)的图象在y轴右侧的最高点从左到右依次为B1、B2、B3、…,与x轴正半轴的交点从左到右依次为C1、C2、C3、….
如图,已知函数f(x)=msin($\frac{π}{2}$x+$\frac{π}{4}$)(m>0)的图象在y轴右侧的最高点从左到右依次为B1、B2、B3、…,与x轴正半轴的交点从左到右依次为C1、C2、C3、….查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 |
| y | 1 | 4 | 6 | 8 | 11 |
| A. | $\widehat{y}$=2x-1 | B. | $\widehat{y}$=2x+1 | C. | $\widehat{y}$=2.4x-1.2 | D. | $\widehat{y}$=2.4x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | -$\frac{π}{6}$ | $\frac{π}{3}$ | $\frac{5π}{6}$ | $\frac{4π}{3}$ | $\frac{11π}{6}$ | $\frac{7π}{3}$ | $\frac{17π}{6}$ |
| y | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com