
分析 (Ⅰ)由OM=ON得原点O在MN的中垂线上,由圆的弦中点性质和直线垂直的条件列出方程,求出t的值和C的坐标,代入圆的标准方程化简,再验证直线与圆的位置关系;
(Ⅱ)根据三边关系判断出取最大值的条件,由圆外一点与圆上一点距离最值问题求出最大值,由点斜式方程求出BC的直线方程,以及此时点P的坐标.
解答 解:(Ⅰ)∵OM=ON,所以,则原点O在MN的中垂线上.
设MN的中点为H,则CH⊥MN,--------------------(1分)
∴C、H、O三点共线,
∵直线MN的方程是3x+y-4=0,
∴直线OC的斜率$k=\frac{{\frac{3}{t}}}{t}$=$\frac{3}{t^2}$=$\frac{1}{3}$,解得t=3或t=-3,
∴圆心为C(3,1)或C(-3,-1)-------------------------(4分)
∴圆C的方程为(x-3)2+(y-1)2=10或(x+3)2+(y+1)2=10
由于当圆方程为(x+3)2+(y+1)2=10时,圆心到直线3x+y-4=0的距离d>r,
此时不满足直线与圆相交,故舍去,
∴圆C的方程为(x-3)2+(y-1)2=10-------------------------(6分)
(Ⅱ) 在三角形PBQ中,两边之差小于第三边,故|PQ|-|PB|≤|BQ|
又B,C,Q三点共线时|BQ|最大-----------------------(9分)
所以,|PQ|-|PB|的最大值为$|{BC}|+\sqrt{10}=2\sqrt{10}$,
∵B(0,2),C(3,1),∴直线BC的方程为$y=-\frac{1}{3}x+2$,
∴直线BC与直线x+y+2=0的交点P的坐标为(-6,4)---------------------(12分)
点评 本题考查了直线与圆的位置关系,直线垂直的条件,圆的性质,以及圆外一点与圆上一点距离最值问题等,考查转化思想.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:选择题
 已知函数y=loga(x+b)(a,b为常数)的图象如图所示,则函数g(x)=b${\;}^{{x}^{2}-2x}$,x∈[0,3]的最大值是( )
已知函数y=loga(x+b)(a,b为常数)的图象如图所示,则函数g(x)=b${\;}^{{x}^{2}-2x}$,x∈[0,3]的最大值是( )| A. | 1 | B. | b | C. | b2 | D. | $\frac{1}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,3] | B. | (-∞,-3] | C. | [-3,+∞) | D. | (-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | 2-a<2-b | C. | a2>b2 | D. | ac≥bc |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
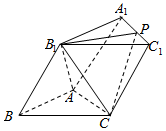 如图,三棱柱ABC-A1B1C1的各棱长为2,侧面BCC1B1⊥底面ABC,∠B${\;}_{{1}_{\;}}$BC=60°,P为A1C1的中点.
如图,三棱柱ABC-A1B1C1的各棱长为2,侧面BCC1B1⊥底面ABC,∠B${\;}_{{1}_{\;}}$BC=60°,P为A1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 性别 对游戏态度 | 男生 | 女生 | 合计 |
| 喜欢玩电脑游戏 | 20 | 5 | 25 |
| 不喜欢玩电脑游戏 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com