
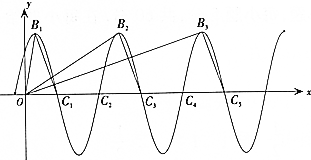
 如图,已知函数f(x)=msin($\frac{π}{2}$x+$\frac{π}{4}$)(m>0)的图象在y轴右侧的最高点从左到右依次为B1、B2、B3、…,与x轴正半轴的交点从左到右依次为C1、C2、C3、….
如图,已知函数f(x)=msin($\frac{π}{2}$x+$\frac{π}{4}$)(m>0)的图象在y轴右侧的最高点从左到右依次为B1、B2、B3、…,与x轴正半轴的交点从左到右依次为C1、C2、C3、….分析 (1)利用正弦函数的图象的特征求得B1、B2、B3、…,与C1、C2、C3、…的坐标,利用两个向量的数量积公式求得$\overrightarrow{O{B}_{1}}$•$\overrightarrow{{B}_{1}{C}_{1}}$的值.
(2)由题意可得∠OB3C5为锐角,且∠OB4C7为钝角,故有${{OB}_{3}}^{2}$+${{{B}_{3}C}_{5}}^{2}$-OC5>0,且 ${{OB}_{4}}^{2}$+${{{B}_{4}C}_{7}}^{2}$-OC7<0,从而求得m的范围.
解答 解:(1)若m=1,则令$\frac{π}{2}$x+$\frac{π}{4}$分别等于$\frac{π}{2}$,$\frac{5π}{2}$,$\frac{9π}{2}$…,
可得B1($\frac{1}{2}$,1)、B2($\frac{9}{2}$,1)、B3($\frac{17}{2}$,1)…,
令$\frac{π}{2}$x+$\frac{π}{4}$分别等于π,2π,3π,…,C1($\frac{3}{2}$,0)、C($\frac{7}{2}$,0)、C3($\frac{11}{2}$,0)…,
∴$\overrightarrow{O{B}_{1}}$•$\overrightarrow{{B}_{1}{C}_{1}}$=($\frac{1}{2}$,1)•(1,-1)=$\frac{1}{2}$-1=-$\frac{1}{2}$.
(2)由题意可得 函数f(x)=msin($\frac{π}{2}$x+$\frac{π}{4}$)(m>0)的周期为$\frac{2π}{\frac{π}{2}}$=4,
△OB3C5为锐角三角形,且△OB4C7为钝角角三角形,即∠OB3C5为锐角,且∠OB4C7为钝角,
∴${{OB}_{3}}^{2}$+${{{B}_{3}C}_{5}}^{2}$-OC5>0,且 ${{OB}_{4}}^{2}$+${{{B}_{4}C}_{7}}^{2}$-OC7<0,
即 ${(\frac{\frac{15}{2}+\frac{19}{2}}{2})}^{2}$+m2+${(\frac{1}{4}•4)}^{2}$+m2-${(\frac{19}{2})}^{2}$>0,且 ${(\frac{\frac{23}{2}+\frac{27}{2}}{2})}^{2}$+m2+${(\frac{1}{4}•4)}^{2}$+m2-${(\frac{27}{2})}^{2}$<0,
求得$\sqrt{\frac{17}{2}}$<m<$\sqrt{\frac{25}{2}}$,即$\frac{\sqrt{34}}{2}$<m<$\frac{5\sqrt{2}}{2}$.
点评 本题主要考查正弦函数的图象的特征,两个向量的数量积公式,锐角三角形、钝角三角形的性质,属于中档题.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 性别 对游戏态度 | 男生 | 女生 | 合计 |
| 喜欢玩电脑游戏 | 20 | 5 | 25 |
| 不喜欢玩电脑游戏 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
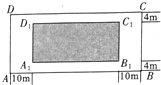 随着我市九龙江南岸江滨路建设的持续推进,未来市民将新增又一休闲好去处,据悉南江滨路建设工程规划配套建造一个长方形公园ABCD,如图所示,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成,已知休闲区A1B1C1D1的面积为4000m2,人行道的宽度分别为4m和10m.
随着我市九龙江南岸江滨路建设的持续推进,未来市民将新增又一休闲好去处,据悉南江滨路建设工程规划配套建造一个长方形公园ABCD,如图所示,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成,已知休闲区A1B1C1D1的面积为4000m2,人行道的宽度分别为4m和10m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com