
某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)= x2+10x(万元).当年产量不小于80千件时,C(x)=51x+
x2+10x(万元).当年产量不小于80千件时,C(x)=51x+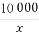 -1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
-1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式.
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
(1) L(x)=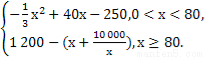
(2) 当产量为100千件时,该厂在这一商品的生产中所获利润最大,最大利润为1000万元.
【解析】(1)因为每件商品售价为0.05万元,则x千件商品销售额为0.05×1000x万元,依题意得:当0<x<80时,L(x)=(0.05×1000x)-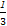 x2-10x-250=
x2-10x-250=
-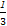 x2+40x-250.
x2+40x-250.
当x≥80时,L(x)=(0.05×1000x)-51x-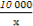 +1450-250=1200-(x+
+1450-250=1200-(x+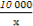 ).
).
所以L(x)=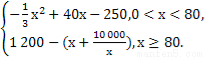
(2)当0<x<80时,L(x)=-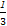 (x-60)2+950.
(x-60)2+950.
此时,当x=60时,L(x)取得最大值,L(60)=950万元.
当x≥80时,L(x)=1200-(x+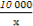 )≤1200-2
)≤1200-2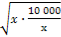 =1200-200=1000,
=1200-200=1000,
此时,当x=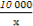 时,即x=100时,L(x)取得最大值1000万元.
时,即x=100时,L(x)取得最大值1000万元.
∵950<1000,
所以,当产量为100千件时,该厂在这一商品的生产中所获利润最大,最大利润为1000万元.


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十第二章第七节练习卷(解析版) 题型:填空题
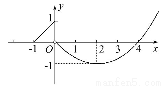
如图,定义在[-1,+∞)上的函数f(x)的图象由一条线段及抛物线的一部分组成,则f(x)的解析式为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十八第三章第二节练习卷(解析版) 题型:填空题
已知α是第三象限角,且cos(85°+α)= ,则sin(α-95°)= .
,则sin(α-95°)= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十五第二章第十二节练习卷(解析版) 题型:填空题
设函数f(x)=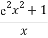 ,g(x)=
,g(x)=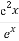 ,对任意x1,x2∈(0,+∞),不等式
,对任意x1,x2∈(0,+∞),不等式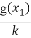 ≤
≤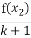 恒成立,则正数k的取值范围是 .
恒成立,则正数k的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十五第二章第十二节练习卷(解析版) 题型:选择题
若0<x< ,则4x与3sin2x的大小关系是( )
,则4x与3sin2x的大小关系是( )
(A)4x>3sin2x (B)4x<3sin2x
(C)4x=3sin2x (D)与x的取值有关
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十二第二章第九节练习卷(解析版) 题型:选择题
如图,A,B,C,D是某煤矿的四个采煤点,m是公路,图中所标线段为道路,ABQP,BCRQ,CDSR近似于正方形.已知A,B,C,D四个采煤点每天的采煤量之比约为5∶1∶2∶3,运煤的费用与运煤的路程、所运煤的质量都成正比.现要从P,Q,R,S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在( )
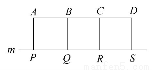
(A)P点 (B)Q点 (C)R点 (D)S点
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十九第三章第三节练习卷(解析版) 题型:填空题
给出如下五个结论:
①存在α∈(0,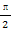 ),使sinα+cosα=
),使sinα+cosα= ;
;
②存在区间(a,b),使y=cosx为减函数而sinx<0;
③y=tanx在其定义域内为增函数;
④y=cos2x+sin(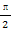 -x)既有最大值和最小值,又是偶函数;
-x)既有最大值和最小值,又是偶函数;
⑤y=sin|2x+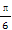 |的最小正周期为π.
|的最小正周期为π.
其中正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十三第二章第十节练习卷(解析版) 题型:解答题
求下列各函数的导数:
(1)y=(x+1)(x+2)(x+3).
(2)y=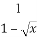 +
+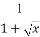 .
.
(3)y=e-xsin2x.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十一第二章第八节练习卷(解析版) 题型:选择题
方程lnx=6-2x的根必定属于区间( )
(A)(-2,1) (B)( ,4)
,4)
(C)(1, ) (D)(
) (D)( ,
, )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com