
| A. | Ax+By+(C1-2C2)=0 | B. | Ax+By+(C2-2C1)=0 | C. | Ax+By+(2C2-C1)=0 | D. | Ax+By+(2C1-C2)=0 |
分析 设直线l1:Ax+By+C1=0关于直线l2:Ax+By+C2=0(C1≠C2)的对称直线为:Ax+By+C3=0,根据C1+C3 =2C2 ,求得 C3 的值,可得对称直线的方程.
解答 解:由于直线l1:Ax+By+C1=0和直线l2:Ax+By+C2=0(C1≠C2)平行,
设直线l1:Ax+By+C1=0关于直线l2:Ax+By+C2=0(C1≠C2)的对称直线为直线l3:Ax+By+C3=0,
则根据直线l2:到直线直线l1的距离等于它到直线l3的距离,可得C1+C3 =2C2 ,
∴C3 =2C2-C1,故对称直线为:Ax+By+2C2 -C1=0,
故选:C.
点评 本题主要考查求一条直线关于它的一条平行直线的对称直线方程的方法,三条平行直线互相平行的性质,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若l⊥m,m⊆α则l⊥α | B. | 若l∥α,m⊆α则l∥m | C. | 若l⊥α,l∥m则m⊥α | D. | 若l∥α,m∥α则l∥m |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
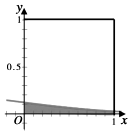 在如图所示的正方形中随机选择10000个点,则选点落入阴影部分(边界曲线C为正态分布N(-1,1)的密度曲线的一部分)的点的个数的估计值为( )
在如图所示的正方形中随机选择10000个点,则选点落入阴影部分(边界曲线C为正态分布N(-1,1)的密度曲线的一部分)的点的个数的估计值为( )| A. | 906 | B. | 1359 | C. | 2718 | D. | 3413 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{3}{π}$ | C. | 3 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com