
分析 先根据圆C1的方程找出圆心坐标与半径R的值,找出圆C2的半径的最大时的情况:当圆c2的圆心Q为线段AB的中点时,圆c2与圆C1相切,切点在圆C1的劣弧$\widehat{AB}$上,设切点为P,此时圆C2的半径r的最大.求r的方法是,联立直线与圆的方程,消去y后得到关于x的一元二次方程,利用韦达定理求出Q的横坐标,把Q的横坐标代入直线方程即可求出Q的纵坐标,得到Q的坐标,利用两点间的距离公式求出两圆心的距离OQ等于d,然后根据两圆内切时,两圆心之间的距离等于两半径相减可得圆C2的半径最大值.
解答 解:由圆C1:x2+y2=9,可得圆心O(0,0),半径R=3,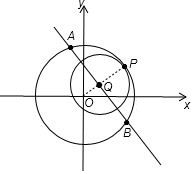
如图,当圆c2的圆心Q为线段AB的中点时,圆c2与圆C1相切,切点在圆C1的劣弧$\widehat{AB}$上,设切点为P,此时圆C2的半径r的最大.
联立直线与圆的方程得$\left\{\begin{array}{l}{3x+4y-5=0}\\{{x}^{2}+{y}^{2}=9}\end{array}\right.$,
消去y得到25x2-30x-119=0,
设A(x1,y1),B(x2,y2),则x1+x2=$\frac{6}{5}$,
∴线段AB的中点Q的横坐标为$\frac{3}{5}$,把x=$\frac{3}{5}$代入直线方程中解得y=$\frac{4}{5}$,
∴Q($\frac{3}{5}$,$\frac{4}{5}$),∴两圆心之间的距离OQ=d=$\sqrt{(\frac{3}{5})^{2}+(\frac{4}{5})^{2}}$=1,
∵两圆内切,所以圆c2的最大半径r=R-d=3-1=2.
此时C2C1所在的直线方程为:$\frac{y}{x}=\frac{\frac{4}{5}}{\frac{3}{5}}$=$\frac{4}{3}$,即4x-3y=0.
故答案为:2,4x-3y=0.
点评 此题考查学生掌握两圆内切时两半径所满足的条件,灵活运用韦达定理及两点间的距离公式化简求值,是一道中档题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| 第一次月考物理成绩 | 第二次月考物理成绩 | 第三次月考物理成绩 | |
| 学生甲 | 80 | 85 | 90 |
| 学生乙 | 81 | 83 | 85 |
| 学生丙 | 90 | 86 | 82 |
| A. | 甲、乙、丙第三次月考物理成绩的平均数为86 | |
| B. | 在这三次月考物理成绩中,甲的成绩平均分最高 | |
| C. | 在这三次月考物理成绩中,乙的成绩最稳定 | |
| D. | 在这三次月考物理成绩中,丙的成绩方差最大 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在实数x0,使得g(x0)=1 | B. | 当x1<x2时,必有g(x1)<g(x2) | ||
| C. | g(2)的取值与实数a有关 | D. | 函数g(f(x))的图象必过定点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | Ax+By+(C1-2C2)=0 | B. | Ax+By+(C2-2C1)=0 | C. | Ax+By+(2C2-C1)=0 | D. | Ax+By+(2C1-C2)=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
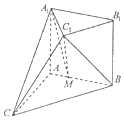 如图,在多面体ABCA1B1C1中,四边形ABB1A1是正方形,CA⊥平面ABB1A1,AC=AB=1,B1C1∥BC,BC=2B1C1.
如图,在多面体ABCA1B1C1中,四边形ABB1A1是正方形,CA⊥平面ABB1A1,AC=AB=1,B1C1∥BC,BC=2B1C1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com