
 中,角
中,角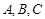 所对的边分别为
所对的边分别为 ,若
,若 。
。 ;
; 的平分线交
的平分线交 于
于 ,且
,且 ,求
,求 的值。
的值。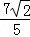 .
. 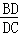 =
=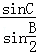 ,由第一问知道C=B,
,由第一问知道C=B,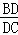 ="2cos"
="2cos" 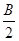 . 8分
. 8分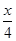 =45°.--9分
=45°.--9分 ,∴
,∴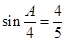 ,
,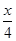 )=cos45°cos
)=cos45°cos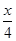 +sin45°sin
+sin45°sin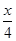 =
=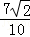 .
.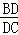 =2cos
=2cos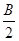 =2cosα=
=2cosα=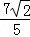 . 12分
. 12分

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com