练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若x＋y＝4，x＞0，y＞0，则lgx＋lgy的最大值是      。

     

    【答案】

    lg4.

    【解析】

    试题分析：lgx＋lgy=lgxy≤lg()2=lg4.

    考点：本题主要考查均值定理的应用、对数的性质。

    点评：应用均值定理，应注意“一正、二定、三相等”。常见错误是忽视等号成立的条件。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：学习周报　数学　北师大课标高一版(必修4)　2009－2010学年　第46期　总202期 北师大课标版 题型：013

    已知{a，b}为一组基底，若实数x，y满足xa＋(2－y)b＝a＋2b，则有

    [　　]
    A．

    x＝0，y＝0

    B．

    x＝0，y＝4

    C．

    x＝1，y＝0

    D．

    x＝1，y＝4

    查看答案和解析>>

    科目：高中数学 来源：汕头市2007年普通高校招生模拟考试(二)、理科数学 题型：044

    解答题：解答应写出文字说明，证明过程或演算步骤．

    定义F(x，y)＝(1＋x)y，x，y∈(0，＋∞)，

    (Ⅰ)令函数f(x)＝F(1，log2(x2－4x＋9))的图象为曲线C1，曲线C1与y轴交于点A(0，m)，过坐标原点O向曲线C1作切线，切点为B(n，t)(n＞0)，设曲线C1在点A、B之间的曲线段与线段OA、OB所围成图形的面积为S，求S的值；

    (Ⅱ)令函数g(x)＝F(1，log2(x3＋ax2＋bx＋1))的图象为曲线C2，若存在实数b使得曲线C2在x0(－4＜x0＜－1)处有斜率为－8的切线，求实数a的取值范围；

    (Ⅲ)当且x＜y时，证明F(x，y)＞F(y，x)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若x＋y＝4，x＞0，y＞0，则lgx＋lgy的最大值是      。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

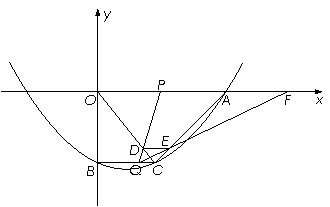
    如图，在平面直角坐标系xoy中，抛物线y＝x 2－x－10与x轴的交点为A，与y轴的交点为点B，过点B作x轴的平行线BC，交抛物线于点C，连结AC．现有两动点P，Q分别从O，C两点同时出发，点P以每秒4个单位的速度沿OA向终点A移动，点Q以每秒1个单位的速度沿CB向点B移动，点P停止运动时，点Q也同时停止运动．线段OC，PQ相交于点D，过点D作DE∥OA，交CA于点E，射线QE交x轴于点F．设动点P，Q移动的时间为t(单位：秒)

    （1）求A，B，C三点的坐标和抛物线的顶点坐标；

    （2）当t为何值时，四边形PQCA为平行四边形？请写出计算过程；

    （3）当t∈（0，）时，△PQF的面积是否总为定值？若是，求出此定值；若不是，请说明理由；

    （4）当t为何值时，△PQF为等腰三角形？请写出解答过程．

     


    查看答案和解析>>

    同步练习册答案