
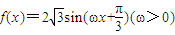 .
. 是最小正周期为π的偶函数,求ω和θ的值;
是最小正周期为π的偶函数,求ω和θ的值;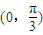 上是增函数,求ω的最大值;并求此时f(x)在[0,π]上的取值范围.
上是增函数,求ω的最大值;并求此时f(x)在[0,π]上的取值范围.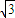 sin(ωx+ωθ+
sin(ωx+ωθ+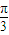 )(0<θ<
)(0<θ< )是最小正周期为π的偶函数,利用周期公式与诱导公式即可求得ω和θ的值;
)是最小正周期为π的偶函数,利用周期公式与诱导公式即可求得ω和θ的值;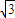 sin(3ωx+
sin(3ωx+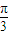 ),利用正弦函数的单调性可求ω的最大值;并求此时f(x)在[0,π]上的取值范围.
),利用正弦函数的单调性可求ω的最大值;并求此时f(x)在[0,π]上的取值范围. sin(ωx+
sin(ωx+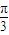 )(0<θ<
)(0<θ<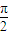 ),
), sin(ωx+ωθ+
sin(ωx+ωθ+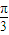 )(0<θ<
)(0<θ<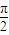 ),
), =kπ+
=kπ+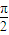 ,(k∈Z),又0<θ<
,(k∈Z),又0<θ< ,
,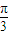 <2θ+
<2θ+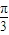 <
<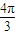 .
. .
.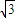 sin(3ωx+
sin(3ωx+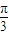 )在(0,
)在(0, )上是增函数,
)上是增函数, ≤3ωx+
≤3ωx+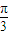 ≤2kπ+
≤2kπ+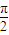 (k∈Z),ω>0得:
(k∈Z),ω>0得: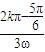 ≤x≤
≤x≤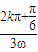 (k∈Z),
(k∈Z),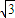 sin(3ωx+
sin(3ωx+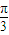 )在(0,
)在(0,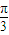 )上是增函数,
)上是增函数,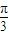 ≤
≤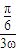 ,
, .
. .
. 时,f(x)=2
时,f(x)=2 sin(
sin( x+
x+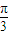 ).
). x+
x+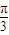 ∈[
∈[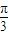 ,
,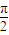 ],
],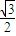 ≤sin(
≤sin( x+
x+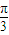 )≤1.
)≤1. sin(
sin( x+
x+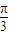 )≤2
)≤2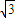 .
.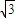 sin(
sin( x+
x+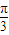 )∈[3,2
)∈[3,2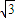 ].
].

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源:2013-2014学年上海市长宁区高三上学期教学质量检测理科数学试卷(解析版) 题型:解答题
已知函数 ,
,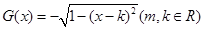
(1)若 是常数,问当
是常数,问当 满足什么条件时,函数
满足什么条件时,函数 有最大值,并求出
有最大值,并求出 取最大值时
取最大值时 的值;
的值;
(2)是否存在实数对 同时满足条件:(甲)
同时满足条件:(甲) 取最大值时
取最大值时 的值与
的值与 取最小值的
取最小值的 值相同,(乙)
值相同,(乙) ?
?
(3)把满足条件(甲)的实数对 的集合记作A,设
的集合记作A,设 ,求使
,求使 的
的 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013年上海市四区(静安、杨浦、青浦、宝山)高考二模理科数学试卷(解析版) 题型:解答题
已知函数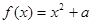 .
.
(1)若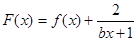 是偶函数,在定义域上
是偶函数,在定义域上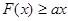 恒成立,求实数
恒成立,求实数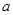 的取值范围;
的取值范围;
(2)当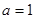 时,令
时,令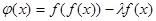 ,问是否存在实数
,问是否存在实数 ,使
,使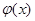 在
在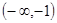 上是减函数,在
上是减函数,在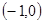 上是增函数?如果存在,求出
上是增函数?如果存在,求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013届安徽省蚌埠市高二下学期期中联考理科数学试卷(解析版) 题型:解答题
(本题满分12分)
已知函数 ,
,
(1)若 是
是 的极值点,求
的极值点,求 值;
值;
(2)若函数 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com