
(09年临沭县模块考试理)(12分)
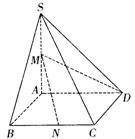
如图,在四棱锥S―ABCD中,底面ABCD是边长为1的菱形,∠ABC=![]() ,SA⊥底面
,SA⊥底面
ABCD,SA=2,M 的为SA的中点,N在线段BC上。
(Ⅰ)当![]() 为何值时,MN∥平面SCD;(说明理由)。
为何值时,MN∥平面SCD;(说明理由)。
(Ⅱ)求MD和平面SCD所成角的正弦值。
解析:(Ⅰ)法一:当![]() =
=![]() 时,MN∥平面SCD。 ????????????????1分
时,MN∥平面SCD。 ????????????????1分
证明如下:取SB中点E,连线ME,NE ????????????????2分
则ME∥AB,又∵AB∥CD
∴ME∥CD ????????????????3分
又∵NE∥SC ????????????????4分
∵ME∩NE=E
∴平面MNE∥平面SCD ????????????????5分
又MN![]() 平面MNE
平面MNE
∴MN∥平面SCD ????????????????6分
法二:作AP⊥CD于点P(如图),分别以AB、AP、AS所在直线为x、y、z轴建立空间
坐标系。

A(0,0,0),B(1,0,0),
P(0,![]() ,0),D(
,0),D(![]() ,
,![]() ,0),
,0),
S(0,0,2),M(0,0,1),
C(1![]() ,
,![]() ,0),
,0),
设![]()
∴![]() (
(![]() ,
,![]() ,0)
,0)
=![]() ?????????????????3分
?????????????????3分
![]() ?????????????????4分
?????????????????4分
设平面SCD的法向量为![]() ,则
,则
![]()
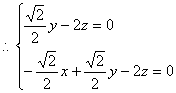
取![]() ,得
,得![]() ?????????????????5分
?????????????????5分
∵![]()
∴![]() =
=![]() ,即N为BC中点时,MN∥平面SCD ?????????????????6分
,即N为BC中点时,MN∥平面SCD ?????????????????6分
(Ⅱ)∵![]() ?????????????????7分
?????????????????7分
又∵平面SCD的法向量为![]() ?????????????????9分
?????????????????9分
∴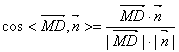 ????????????????10分
????????????????10分
=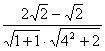 =
=![]() ????????????????11分
????????????????11分
∴MD和平面SCD所成角的正弦值为![]() ?????????????????12分
?????????????????12分


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
(09年临沭县模块考试理)(14分)
已知函数f(x)与g(x)=alnx-x2(a为常数)的图象关于直线x=1对称,且x=1是f(x)的一个极值点。
(Ⅰ)求出函数f(x)的表达式和单调区间;
(Ⅱ)若已知当![]() 时,不等式
时,不等式![]() 恒成立,求m的取值范围。(注:若
恒成立,求m的取值范围。(注:若![]() )。
)。
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年临沭县模块考试理)(12分)已知F1、F2是椭圆![]() 的左、右焦点,O为坐标原点,点P
的左、右焦点,O为坐标原点,点P![]() 在椭圆上,线段PF2与y轴的交点M满足
在椭圆上,线段PF2与y轴的交点M满足![]()
(Ⅰ)求椭圆的标准方程
(Ⅱ)⊙O是F1F2为直径的圆,一直线l:y=kx+m与⊙O相切,并与椭圆交与不同的两
点A,B,当![]() 时,求△AOB的面积S。
时,求△AOB的面积S。
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年临沭县模块考试理)(12分)
已知数列{an}的前n项和![]() 。
。
(Ⅰ)用n、k表示an;
(Ⅱ)若数列{bn}对任意正整数n,均有(bn+1-bn+2)lna1+(bn+2-bn)lna3+(bn-bn+1)lna5=0,
求证:数列{bn}为等差数列
(Ⅲ)在(Ⅰ)、(Ⅱ)中,设k=1,bn=n+1,xn=a1b1+a2b2+???+anbn,试求数列{xn}的通
项公式。
查看答案和解析>>
科目:高中数学 来源: 题型:
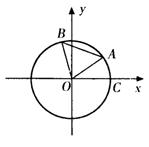
(09年临沭县模块考试理)(12分)
如图点A,B是单位圆上的两点,A,B点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为![]() ,记∠COA=α。
,记∠COA=α。
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com