练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    求函数f(x)＝3x2－x＋2(x∈[1，3])的值域．

    答案：
    解析：

    　　解：因为函数f(x)＝3x2－x＋2在[1，3]上单调递增，

    　　所以当x＝1时，所给函数有最小值，为f(1)＝3－1＋2＝4；当x＝3时，所给函数有最大值，为f(3)＝33－3＋2＝26．

    　　因此，函数f(x)＝3x2－x＋2(x∈[1，3])的值域为[4，26]．

    　　编者按：若题中函数的定义域为R，可用配方法，得f(x)＝3＋，则f(x)的值域为[，＋∞)．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：甘肃省会宁四中2009－2010学年高一上学期期中考试数学试题 题型：044

    求函数f(x)＝3x|x|－6x的单调区间

    查看答案和解析>>

    科目：高中数学 来源：学习周报　数学　人教课标高一版(A必修1)　2009－2010学年　第12期　总168期 人教课标高一版 题型：044

    借助计算器用二分法求函数f(x)＝3x－在区间(0，1)内的零点(精确度0.1)．

    查看答案和解析>>

    科目：高中数学 来源：张家港市后塍高级中学2007～2008第一学期高三数学十二月调研测试卷 题型：022

    用二分法求函数f(x)＝3x－x－4的一个零点，其参考数据如下：

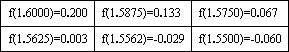
    据此数据，可得方程3x－x－4＝0的一个近似解(精确到0.01)为________．

    查看答案和解析>>

    科目：高中数学 来源：2012年人教A版高中数学必修三1.2基本算法语句练习卷（一）（解析版） 题型：解答题

    已知函数f(x)＝3x－1，求f[f(2)]的值，设计一个程序，解决上述问题．

     

    查看答案和解析>>

    科目：高中数学 来源：2012年人教A版高中数学必修一3.1函数与方程练习卷（二）（解析版） 题型：填空题

    用二分法求函数f(x)＝3x－x－4的一个零点，其参考数据如下：

    f(1.6000)＝0.200

    f(1.5875)＝0.133

    f(1.5750)＝0.067

    f(1.5625)＝0.003

    f(1.5562)＝－0.029

    f(1.5500)＝－0.060

    据此数据，可得方程3x－x－4＝0的一个近似解(精确到0.01)为________．

     

    查看答案和解析>>

    同步练习册答案