
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
已知点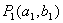 ,
,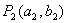 ,
,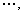
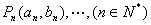 ,都在函数
,都在函数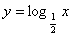 的图像上.
的图像上.
(1)若数列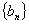 是等差数列,求证:数列
是等差数列,求证:数列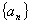 是等比数列;
是等比数列;
(2)若数列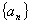 的前
的前 项和是
项和是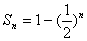 ,设过点
,设过点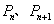 的直线与坐标轴所围成的三角形面积为
的直线与坐标轴所围成的三角形面积为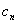 ,求
,求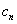 的最大值;
的最大值;
(3)若存在一个常数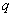 ,使得对任意的正整数
,使得对任意的正整数 都有
都有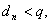 且
且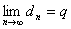 ,则称
,则称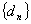 为“左逼近”数列,
为“左逼近”数列,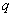 为该数列的“左逼近”值. 若数列
为该数列的“左逼近”值. 若数列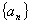 的前
的前 项和是
项和是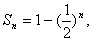 设数列
设数列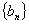 的前
的前 项和是
项和是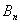 ,且
,且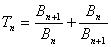 ,
,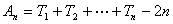 ,试判断数列
,试判断数列 是否为“左逼近”数列,如果是,求出“左逼近”值;如果不是,说明理由.
是否为“左逼近”数列,如果是,求出“左逼近”值;如果不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
某段城铁线路上依次有A,B,C三站,AB=5km,BC=3km在列车运行时刻表上,规定列车8时整从A站发车,8时07分到达B站并停车1分钟,8时12分到达C站,在实际运行时,假设列车从A站正点发车,在B站停留1分钟,并在行驶时以同一速度vkm/h,匀速行驶,列车从A站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差.
(1)分别写出列车在B、C两站的运行误差;
(2)若要求列车在B,C两站的运行误差之和不超过2分钟,求v的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知f(x)=ax2+bx+c,其中a∈N,b,c∈Z.
(1)若b>2a,在[-1,1]上是否存在x使得|f(x|>b成立.
(2)当方程f(x)-x=0的根在(0,1)内时,试求a的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com