
在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C: (a>0),过点P(-2,-4)的直线l的参数方程为
(a>0),过点P(-2,-4)的直线l的参数方程为 (t为参数),l与C分别交于M,N.
(t为参数),l与C分别交于M,N.
(1)写出C的平面直角坐标系方程和l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求a的值.
(1)x-y-2=0;(2)1.
【解析】试题分析:(1)利用极坐标与普通方程的关系式,可得C为抛物线方程,消去参数t,可得直线l的方程;(2)由|PM|=|t1|,|MN|=|t1-t2|,|PN|=|t2|成等比数列,可转化为关于a的等量关系求解.
试题解析:(Ⅰ)曲线C的直角坐标方程为y2=2ax(a>0);
直线l的普通方程为x-y-2=0. 4分
(Ⅱ)将直线l的参数方程与C的直角坐标方程联立,得
t2-2(4+a) t+8(4+a)=0 (*)
t+8(4+a)=0 (*)
△=8a(4+a)>0.
设点M,N分别对应参数t1,t2,恰为上述方程的根.
则|PM|=|t1|,|PN|=|t2|,|MN|=|t1-t2|.
由题设得(t1-t2)2=|t1t2|,即(t1+t2)2-4t1t2=|t1t2|.
由(*)得t1+t2=2(4+a)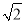 ,t1t2=8(4+a)>0,则有
,t1t2=8(4+a)>0,则有
(4+a)2-5(4+a)=0,得a=1,或a=-4.
因为a>0,所以a=1. 10分
考点:参数方程与极坐标


科目:高中数学 来源:2015届河北省高二下学期第一次月考理科数学试卷(解析版) 题型:解答题
(满分12分)已知函数 .
.
(1)当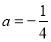 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)若函数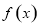 在区间
在区间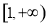 上为减函数,求实数
上为减函数,求实数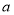 的取值范围;
的取值范围;
(3)当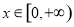 时,不等式
时,不等式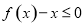 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届河北省唐山市高三年级摸底考试理科数学试卷(解析版) 题型:选择题
已知a>0,且a≠1,则函数f(x)=ax+(x-1)2-2a的零点个数为( )
A.1 B.2 C.3 D.与a有关
查看答案和解析>>
科目:高中数学 来源:2015届河北省唐山市高三年级摸底考试理科数学试卷(解析版) 题型:选择题
抛物线y=2ax2(a≠0)的焦点是( )
A.( ,0) B.(
,0) B.( ,0)或(-
,0)或(- ,0)
,0)
C.(0,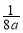 ) D.(0,
) D.(0,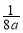 )或(0,-
)或(0,-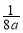 )
)
查看答案和解析>>
科目:高中数学 来源:2015届河北省唐山市高三年级摸底考试文科数学试卷(解析版) 题型:解答题
某公司对夏季室外工作人员规定如下:当气温超过35℃时,室外连续工作时间严禁超过100分钟;不少于60分钟的,公司给予适当补助.随机抽取部分工人调查其高温室外连续工作时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中工作时间范围是[0,100],样本数据分组为[0,20),[20,40),[40.60),[60,80),[80,100].
(1)求频率分布直方图中x的值;
(2)根据频率分布直方图估计样本数据的中位数;
(3)用这个样本的频率分布估计总体分布,将频率视为概率;用分层抽样的方法从享受补助人员和不享受补助人员中抽取25人的样本,检测他们健康状况的变化,那么这两种人员应该各抽取多少人?

查看答案和解析>>
科目:高中数学 来源:2015届河北省唐山市高三年级摸底考试文科数学试卷(解析版) 题型:选择题
已知a>0,x,y满足约束条件 ,且z=2x+y的最小值为1,则a=( )
,且z=2x+y的最小值为1,则a=( )
A.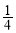 B.
B.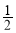 C.1 D.2
C.1 D.2
查看答案和解析>>
科目:高中数学 来源:2015届河北省高二下学期期中考试理科数学试卷(解析版) 题型:填空题
当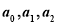 成等差数列时,有
成等差数列时,有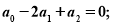 当
当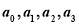 成等差数列时,有
成等差数列时,有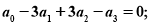 当
当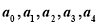
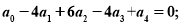 成等差数列时,有由此归纳,当
成等差数列时,有由此归纳,当 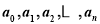 成等差数列时,有
成等差数列时,有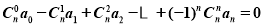 .如果
.如果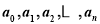 成等比数列,类比上述方法归纳出的等式为______________.
成等比数列,类比上述方法归纳出的等式为______________.
查看答案和解析>>
科目:高中数学 来源:2015届河北省保定市高二下学期期中考试理科数学试卷(解析版) 题型:解答题
设函数 .
.
(1)求 的单调区间和极值;
的单调区间和极值;
(2)若关于 的方程
的方程 有3个不同实根,求实数a的取值范围.
有3个不同实根,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com