
 在[1,+∞)上为增函数.
在[1,+∞)上为增函数.
 <
< ( n∈N*且n≥2 )
( n∈N*且n≥2 )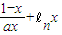 在[1,+∞)上为增函数,所以在[1,+∞)上导数大于等于0恒成立,就可根据x的范围求出a的范围.
在[1,+∞)上为增函数,所以在[1,+∞)上导数大于等于0恒成立,就可根据x的范围求出a的范围.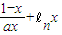 在[1,+∞)上为增函数,所以n≥2时:f(
在[1,+∞)上为增函数,所以n≥2时:f(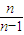 )>f(1),因为f(1)=0,所以,n≥2时:f(
)>f(1),因为f(1)=0,所以,n≥2时:f(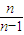 )>0,就可得到
)>0,就可得到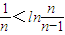 ,进而证明
,进而证明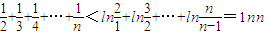 成立,再利用导数判断y=lnx-x在[1,+∞)上为减函数,就可得到n≥2时,ln
成立,再利用导数判断y=lnx-x在[1,+∞)上为减函数,就可得到n≥2时,ln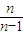 <
<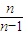 =1+
=1+ (n≥2),
(n≥2),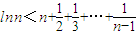 .
.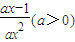
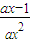 ≥0对x∈[1,+∞)恒成立
≥0对x∈[1,+∞)恒成立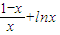 ,
,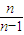 )=
)=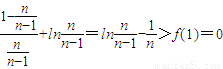

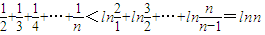
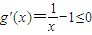 对x∈[1,+∞)恒成立,
对x∈[1,+∞)恒成立,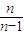 >1
>1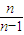 )=ln
)=ln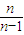 -
-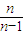 <g(1)=-1<0
<g(1)=-1<0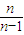 <
<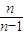 =1+
=1+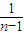 (n≥2)
(n≥2)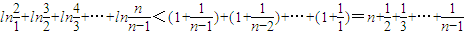
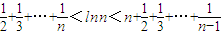 (n∈N*且≥2)成立.
(n∈N*且≥2)成立.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com