
 (a>b>0)的一个焦点F引直线bx-ay=0的垂线,垂足为M,延长FM交y轴于E,若
(a>b>0)的一个焦点F引直线bx-ay=0的垂线,垂足为M,延长FM交y轴于E,若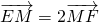 ,则该椭圆的离心率为
,则该椭圆的离心率为



 x
x ,直线的方程是y=-
,直线的方程是y=- (x-c)
(x-c) ,所以E点的坐标(0,
,所以E点的坐标(0, )
)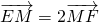 ,
, )=2(c-x,-y)=(2c-2x,-2y)
)=2(c-x,-y)=(2c-2x,-2y)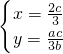
 )
)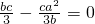
 a2
a2 a.
a. =
=


科目:高中数学 来源: 题型:
A.椭圆左准线与x轴的交点 B.坐标原点
C.椭圆右准线与x轴的交点 D.右焦点
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练24练习卷(解析版) 题型:选择题
过椭圆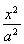 +
+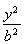 =1(a>b>0)的焦点垂直于x轴的弦长为
=1(a>b>0)的焦点垂直于x轴的弦长为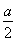 ,则双曲线
,则双曲线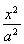 -
-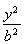 =1的离心率e的值是( )
=1的离心率e的值是( )
(A) 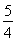 (B)
(B) 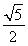
(C) 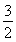 (D)
(D) 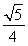
查看答案和解析>>
科目:高中数学 来源:2014届甘肃武威六中高二12月学段检测文科数学试题(解析版) 题型:选择题
已知AB是过椭圆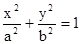 (a>b>0)的左焦点F1的弦,则⊿ABF2的周长是( )
(a>b>0)的左焦点F1的弦,则⊿ABF2的周长是( )
A.a B.2a C.3ª D.4a
查看答案和解析>>
科目:高中数学 来源:2009-2010学年安徽省皖中地区示范高中高三联考数学试卷(文科)(解析版) 题型:选择题
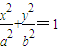 (a>b>0)的焦点且垂直于x轴的直线被椭圆截得的线段长为
(a>b>0)的焦点且垂直于x轴的直线被椭圆截得的线段长为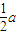 ,则该椭圆的离心率是( )
,则该椭圆的离心率是( )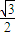



查看答案和解析>>
科目:高中数学 来源:2010年北京市一模试卷及高频考点透析:推理与证明 几何证明选讲(解析版) 题型:解答题
 ,(a>b>0)的两焦点分别为F1、F2,
,(a>b>0)的两焦点分别为F1、F2, ,离心率
,离心率 .过直线l:
.过直线l: 上任意一点M,引椭圆C的两条切线,切点为A、B.
上任意一点M,引椭圆C的两条切线,切点为A、B. (a>b>0),上一点P(x,y)处的切线方程”(只写类比结论,不必证明).
(a>b>0),上一点P(x,y)处的切线方程”(只写类比结论,不必证明). );
);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com