【题目】如图,在四棱锥
中,底面
为平行四边形, 
为侧棱
的中点.
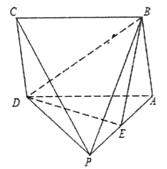
（Ⅰ）求证: 
∥平面
（Ⅱ）若
,
,
求证:平面
平面
【答案】（1）（2）均见解析．
【解析】试题分析：（1）连结AC，交BD于O，连结OE，E为PA的中点，利用三角形中位线的性质，可知OE∥PC，利用线面平行的判定定理，即可得出结论；
（2）先证明PA⊥DE，再证明PA⊥OE，可得PA⊥平面BDE，从而可得平面BDE⊥平面PAB．
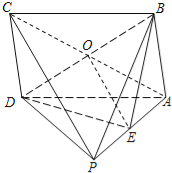
证明：（1）连结AC，交BD于O，连结OE．
因为ABCD是平行四边形，所以OA=OC．…（2分）
因为E为侧棱PA的中点，所以OE∥PC．…（4分）
因为PC平面BDE，OE平面BDE，所以PC∥平面BDE．…（6分）
（2）因为E为PA中点，PD=AD，所以PA⊥DE．…（8分）
因为PC⊥PA，OE∥PC，所以PA⊥OE．
因为OE平面BDE，DE平面BDE，OE∩DE=E，
所以PA⊥平面BDE．…（12分）
因为PA平面PAB，所以平面BDE⊥平面PAB．…（14分）
科目：高中数学 来源： 题型：
【题目】已知有穷数列：
，
，
，……，
的各项均为正数，且满足条件：
①
；②
.
（1）若
，
，求出这个数列；
（2）若
，求
的所有取值的集合；
（3）若
是偶数，求的最大值（用表示）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某高中有高一新生500名，分成水平相同的
两类教学实验，为对比教学效果，现用分层抽样的方法从两类学生中分别抽取了40人，60人进行测试
（1）求该学校高一新生两类学生各多少人？
（2）经过测试，得到以下三个数据图表：
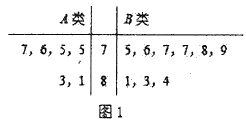
图1：75分以上两类参加测试学生成绩的茎叶图
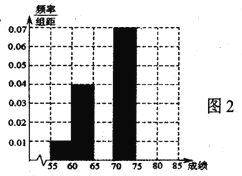
图2：100名测试学生成绩的频率分布直方图
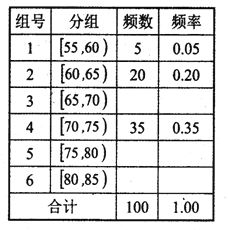
下图表格：100名学生成绩分布表：
①先填写频率分布表中的六个空格，然后将频率分布直方图（图2）补充完整；
②该学校拟定从参加考试的79分以上（含79分）的
类学生中随机抽取2人代表学校参加市比赛，求抽到的2人分数都在80分以上的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的中心在坐标原点，左、右焦点
分别在
轴上，离心率为
，在其上有一动点
，
到点
距离的最小值是1.过
作一个平行四边形，顶点
都在椭圆
上，如图所示.
（Ⅰ）求椭圆
的方程；
（Ⅱ）判断
能否为菱形，并说明理由.
（Ⅲ）当
的面积取到最大值时，判断的形状，并求出其最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
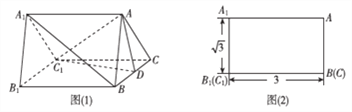
【题目】如图(1)是一个水平放置的正三棱柱
， 
是棱
的中点，正三棱柱的主视图如图(2).
(1)图(1)中垂直于平面
的平面有哪几个(直接写出符合要求的平面即可，不必说明或证明)
(2)求正三棱柱
的体积；
(3)证明： 
平面
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】《九章算术》是我国古代数学成就的杰出代表，其中《方田》章有弧田面积计算问题，计算术曰：以弦乘矢，矢又自乘，并之，二而一．其大意是，弧田面积计算公
式为：弧田面积＝
，弧田是由圆弧（简称为弧田弧）和以圆
弧的两端为顶点的线段（简称为弧田弦）围成的平面图形，公式中“弦”指的是弧
田弦的长，“矢”等于弧田弧所在圆的半径与圆心到弧田弦的距离之差．现有一弧
田，其弦长AB等于6米，其弧所在圆为圆O，若用上述弧田面积计算公式算得该
弧田的面积为
平方米，则cos∠AOB＝ （ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
．
（1）若曲线
在
处的切线方程为
，求实数
的值；
（2）设
，若对任意两个不等的正数
，
，都有
恒成立，求实数
的取值范围；
（3）若在
上存在一点
，使得
成立，求实数
的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
