
分析 (Ⅰ)由MP⊥MQ,则圆心到直线l:x+2y-3=0的距离d=$\frac{\sqrt{2}}{2}$r,即可得到m的值.
(Ⅱ)设P(x1,y1),Q(x2,y2),将x=3-2y代入x2+y2-x-6y+c=0得5y2-16y+6+c=0,利用韦达定理,结合x1x2+y1y2=0,求出c.
解答 解:(Ⅰ)圆的标准方程为(x-$\frac{1}{2}$)2+(y-3)2=$\frac{37}{4}$-c,圆心M($\frac{1}{2}$,3),半径r=$\sqrt{\frac{37}{4}-c}$,
若MP⊥MQ,则圆心到直线l:x+2y-3=0的距离d=$\frac{\sqrt{2}}{2}$r,
即$\frac{|\frac{1}{2}+6-3|}{\sqrt{5}}$=$\frac{\sqrt{2}}{2}$•$\sqrt{\frac{37}{4}-c}$,即c=-$\frac{87}{20}$.
(Ⅱ)设P(x1,y1),Q(x2,y2),将x=3-2y代入x2+y2-x-6y+c=0得5y2-16y+6+c=0,
则y1+y2=$\frac{16}{5}$,y1y2=$\frac{6+c}{5}$.
∵OP⊥OQ,
∴x1x2+y1y2=0.
∴5y1y2-6(y1+y2)+9=0,
∴5•$\frac{6+c}{5}$-6•$\frac{16}{5}$+9=0,
∴c=$\frac{21}{5}$.
点评 此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,平面向量的数量积运算法则,韦达定理,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
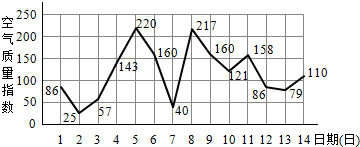 如图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表,某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).
如图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表,某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).| 空气质量指数 | 污染程度 |
| 小于100 | 优良 |
| 大于100且小于150 | 轻度 |
| 大于150且小于200 | 中度 |
| 大于200且小于300 | 重度 |
| 大于300且小于500 | 严重 |
| 大于500 | 爆表 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com