练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    从甲、乙等6名同学中挑选3人参加某公益活动，要求甲、乙至少有1人参加，不同的挑选方法共有（ ）
    A．16种
    B．20种
    C．24种
    D．120种
    【答案】分析：要求甲、乙中至少有1人参加的对立事件是甲和乙都不参加，所以从事件的反面入手来解，从6个同学中挑选3名参加某项公益活动的结果数减去从甲、乙之外的4个同学中挑选3名参加某项公益活动的结果数，即得所求．
    解答：解：：∵从6个同学中挑选3名参加某项公益活动有种不同挑选方法，
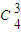
    从甲、乙之外的4个同学中挑选3名参加某项公益活动有 种不同挑选方法；
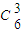
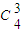
    ∴甲、乙中至少有1人参加，则不同的挑选方法共有- =20-4=16 种不同挑选方法
    故选A．
    点评：此题重点考查组合的意义和组合数公式，由题目中的“至少”知道从反面排除易于解决，这和概率中的对立事件考虑方法一样，正难则反原则．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    从甲、乙等6名同学中挑选3人参加某公益活动，要求甲、乙至少有1人参加，不同的挑选方法共有（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•红桥区一模）从甲、乙等6名同学中挑选3人参加某公益活动，要求甲、乙至少有1人参加，不同的挑选方法共有
    16
    16
    种．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    从甲、乙等6名同学中挑选3人参加某公益活动，要求甲、乙至少有1人参加，不同的挑选方法共有（　　）
    A．16种B．20种C．24种D．120种

    查看答案和解析>>

    科目：高中数学 来源：北京市期末题 题型：单选题

    从甲、乙等6名同学中挑选3人参加某公益活动，要求甲、乙至少有1人参加，不同的挑选方法共有
    [     ]
    A．16种
    B．20种
    C．24种
    D．120种

    查看答案和解析>>

    同步练习册答案