
已知函数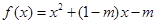
(1)若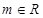 ,解不等式
,解不等式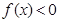 ;
;
(2)若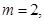 解不等式
解不等式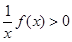
(1)当 时,不等式的解集为:
时,不等式的解集为: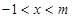
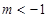 时,不等式的解集为:
时,不等式的解集为: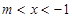
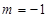 时,不等式的解集为:空集 ;
时,不等式的解集为:空集 ;
(2) {x|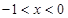 或
或 }。
}。
【解析】
试题分析: (1)根据已知不等式进行因式分解,然后得到方程的根,结合判别式得到不同的解集。
(2)当m=2时,则不等式化为: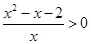 ,将分式化为整式来计算得到。
,将分式化为整式来计算得到。
解:(1) 即为
即为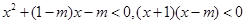
当 时,不等式的解集为:
时,不等式的解集为: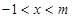
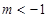 时,不等式的解集为:
时,不等式的解集为: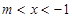
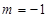 时,不等式的解集为:空集 -----------------------------6分
时,不等式的解集为:空集 -----------------------------6分
(2)当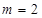 时,不等式化为:
时,不等式化为: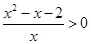 即为:
即为: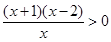
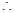 原不等式的解集为:
原不等式的解集为: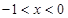 或
或 ----------------------12分
----------------------12分
考点:本题主要考查了一元二次不等式的求解以及函数参数分类讨论思想的运用。
点评:解决该试题的关键是对于m为实数,结合一元二次不等式的求解方法,进行确定出m的三种情况,分类讨论得到。


科目:高中数学 来源: 题型:
已知函数![]()
(1)若函数![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)令![]() ,是否存在实数a,当
,是否存在实数a,当![]() (e是自然常数)时,函数
(e是自然常数)时,函数![]() 的最小值是3,若存在,求出a的值,若不存在,说明理由;
的最小值是3,若存在,求出a的值,若不存在,说明理由;
查看答案和解析>>
科目:高中数学 来源:2014届湖北省荆门市高一下学期期末质量检测数学试卷(解析版) 题型:解答题
已知函数 .
.
(1) 若 ,求使
,求使 时
时 的取值范围;
的取值范围;
(2) 若存在 使
使 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年辽宁省丹东市四校协作体高三第二次联合考试理科数学卷 题型:解答题
(本小题满分12分)
已知函数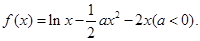
(1)若函数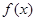 在定义域内单调递增,求
在定义域内单调递增,求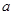 的取值范围;
的取值范围;
(2)若 且关于x的方程
且关于x的方程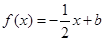 在
在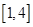 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数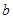 的取值范围;
的取值范围;
(3)设各项为正的数列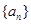 满足:
满足: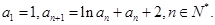 求证:
求证: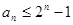
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com