
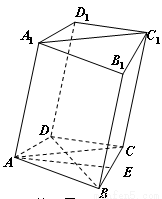
如图,在四棱柱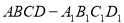 中,已知平面
中,已知平面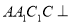 平面
平面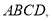 且
且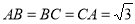 ,
,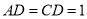 .
.
(1)求证: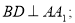
(2)若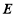 为棱
为棱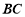 上的一点,且
上的一点,且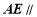 平面
平面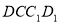 ,求线段
,求线段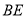 的长度
的长度
 53天天练系列答案
53天天练系列答案科目:高中数学 来源:2013-2014学年江苏省徐州市高三第三次质量检测理科数学试卷(解析版) 题型:解答题
在数列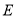 中,已知
中,已知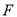 ,
,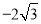 ,
,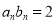 (
(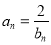 ,
,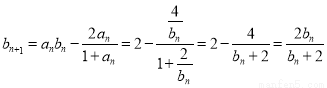 ).
).
(1)当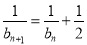 ,
,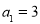 时,分别求
时,分别求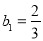 的值,判断
的值,判断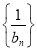 是否为定值,并给出证明;
是否为定值,并给出证明;
(2)求出所有的正整数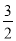 ,使得
,使得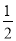 为完全平方数.
为完全平方数.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高考模拟考试文科数学试卷(解析版) 题型:解答题
已知函数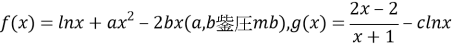 .
.
(1当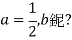 时,
时,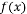 与
与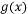 )在定义域上单调性相反,求的
)在定义域上单调性相反,求的 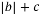 的最小值。
的最小值。
(2)当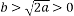 时,求证:存在
时,求证:存在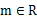 ,使
,使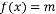 的三个不同的实数解
的三个不同的实数解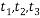 ,且对任意
,且对任意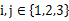 且
且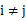 都有
都有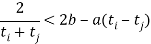 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高考模拟考试文科数学试卷(解析版) 题型:填空题
已知椭圆的中心在坐标原点O, A,C分别是椭圆的上下顶点,B是椭圆的左顶点,F是椭圆的左焦点,直线AF与BC相交于点D。若椭圆的离心率为 ,则∠BDF的正切值
,则∠BDF的正切值
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南通市高三年级第三次模拟考试文科数学试卷(解析版) 题型:解答题
某风景区在一个直径AB为100米的半圆形花园中设计一条观光线路(如图所示).在点A与圆
弧上的一点C之间设计为直线段小路,在路的两侧边缘种植绿化带;从点C到点B设计为沿弧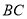 的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
(1)设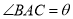 (弧度),将绿化带总长度表示为
(弧度),将绿化带总长度表示为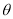 的函数
的函数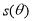 ;
;
(2)试确定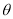 的值,使得绿化带总长度最大.
的值,使得绿化带总长度最大.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com