
已知函数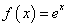 .
.
(I)当 时,设
时,设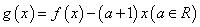 .讨论函数
.讨论函数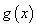 的单调性;
的单调性;
(II)证明当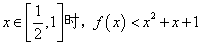 .
.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
已知身穿红、黄两种颜色衣服的各有两人,身穿蓝颜色衣服的有一人,现将这五人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法共有 ( )
A.48种 B.72种 C.78种 D.84种
查看答案和解析>>
科目:高中数学 来源: 题型:
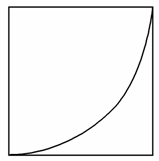
一块正方形薄铁片的边长为4 cm,以它的一个顶点为圆心,边长为半径画弧,沿弧剪下一个扇形(如图),用这块扇形铁片围成一个圆锥筒,则这个圆锥筒的容积等于________cm3.
查看答案和解析>>
科目:高中数学 来源: 题型:
重庆一中高二年级将于4月中旬进行年级辩论赛,每个班将派出6名同学分别担任一辩、二辩、三辩、四辩、五辩和六辩。现某班已有3名男生和3名女生组成了辩论队,按下列要求,能分别安排出多少种不同的辩论顺序?(要求:先列式,再计算,最后用数字作答)
(1)三名男生和三名女生各自排在一起;
(2)男生甲不担任第一辩,女生乙不担任第六辩;
(3)男生甲必须排在第一辩或第六辩,3位女生中有且只有两位排在一起。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com