
 、
、 都是非零向量,且
都是非零向量,且 +3
+3 与7
与7 -5
-5 垂直,
垂直, -4
-4 与7
与7 -2
-2 垂直,求
垂直,求 与
与 的夹角.
的夹角. +3
+3 )•(7
)•(7 -5
-5 )=0且(
)=0且( -4
-4 )•(7
)•(7 -2
-2 )=0,
)=0, 2+16
2+16 •
• -15
-15 2=0…①,
2=0…①, 2-30
2-30 •
• +8
+8 2=0…②
2=0…② •
• =
= 2,代入①式得
2,代入①式得 2=
2= 2,|
2,| |=|
|=| |
| =
=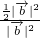 =
= ,
, 与
与 的夹角为60°.
的夹角为60°. +3
+3 )•(7
)•(7 -5
-5 )=0且(
)=0且( -4
-4 )•(7
)•(7 -2
-2 )=0.由此结合数量积的运算性质,化简整理得|
)=0.由此结合数量积的运算性质,化简整理得| |=|
|=| |且2
|且2 •
• =
= 2,再运用向量夹角公式,得到
2,再运用向量夹角公式,得到 、
、 的夹角余弦值,即得
的夹角余弦值,即得 与
与 的夹角大小.
的夹角大小. 、
、 的几个线性组合,在已知两对向量互相垂直的情况下求向量
的几个线性组合,在已知两对向量互相垂直的情况下求向量 与
与 的夹角大小.着重考查了平面向量数量积的公式及其运算性质等知识,属于基础题.
的夹角大小.着重考查了平面向量数量积的公式及其运算性质等知识,属于基础题. 

科目:高中数学 来源: 题型:
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| c |
| OP |
| OA |
| OB |
| OC |
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| a |
| b |
| a |
| b |
| a |
| b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com